题目内容
【题目】合与实践﹣﹣探究图形中角之间的等量关系及相关问题.
问题情境:
正方形ABCD中,点P是射线DB上的一个动点,过点C作CE⊥AP于点E,点Q与点P关于点E对称,连接CQ,设∠DAP=α(0°<α<135°),∠QCE=β.
初步探究:
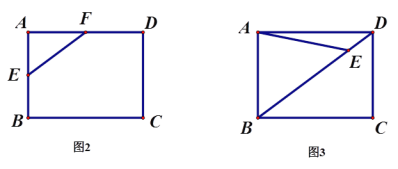
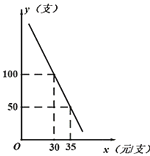
(1)如图1,为探究α与β的关系,勤思小组的同学画出了0°<α<45°时的情形,射线AP与边CD交于点F.他们得出此时α与β的关系是β=2α.借助这一结论可得当点Q恰好落在线段BC的延长线上(如图2)时,α= °,β= °;
深入探究:
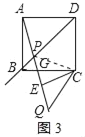
(2)敏学小组的同学画出45°<α<90°时的图形如图3,射线AP与边BC交于点G.请猜想此时α与β之间的等量关系,并证明结论;
拓展延伸:
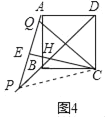
(3)请你借助图4进一步探究:①当90°<α<135°时,α与β之间的等量关系为 ;
②已知正方形边长为2,在点P运动过程中,当α=β时,PQ的长为 .

【答案】(1)30,60;(2)α与β的关系是β=2(90°﹣α);理由见解析;(3)①β=2(α﹣90°);②6﹣2![]() .
.
【解析】
初步探究:(1)连接PC,由对称的性质和等腰三角形的性质得出∠QCE=∠PCE,证明△ABP≌△CBP,得出∠BAP=∠BCP,由平行线得出∠CQE=∠DAP=α,证出α+β=90°①,再证出β=2α②,即可得出结果;
深入探究:(2)连接PC,由对称的性质和等腰三角形的性质得出∠QCE=∠PCE,证明△ABP≌△CBP,得出∠BAP=∠BCP=∠BAD-∠DAP=90°-α,AP=CP,证出∠BAP=∠GCE,得出∠BCG=∠GCE=90°-α,即可得出结论;
拓展延伸:(3)①连接PC,证出∠PCE=∠QCE=β,证明△ABP≌△CBP,得出∠BAP=∠BCP=∠DAP-∠BAD=α-90°,证明∠BAP=∠BCH,得出∠BCP=∠BCH=∠BAP=α-90°,即可得出结论;
②分三种情况:
当0°<α<45°时,β=2α,不合题意;
当45°<α<90°时,β=2(90°-α),得出α=β=60°,作PM⊥AD于M,证出AM=![]() AP,DM=PM=
AP,DM=PM=![]() AM,设AM=x,则CP=AP=2x,DM=PM=
AM,设AM=x,则CP=AP=2x,DM=PM=![]() x,得出方程,解得:x=
x,得出方程,解得:x=![]() ,得出CP=AP=2x=2
,得出CP=AP=2x=2![]() -2,在△PCQ中,求出CE=
-2,在△PCQ中,求出CE=![]() CP=
CP=![]() -1,PE=
-1,PE=![]() CE=3-
CE=3-![]() ,得出PQ=2PE=6-2
,得出PQ=2PE=6-2![]() ;
;
当90°<α<135°时,β=2(α-90°),得出α=β=180°,不合题意.
解:(1)连接PC,如图2所示:

∵点Q与点P关于点E对称,
∴EP=EQ,
∵CE⊥AP,
∴CE垂直平分PQ,
∴CP=CQ,
∴∠QCE=∠PCE,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,AD∥BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中, ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP,
∵AD∥BC,
∴∠CQE=∠DAP=α,
∵CE⊥AP,
∴∠CQE+∠QCE=90°,即α+β=90°①,
∵∠CQE+∠BAP=90°,
∴∠QCE=∠BAP=∠BCP,
∵∠BCP=∠CQE+∠CPQ,
∴β=2α②,
由①②得:α=30°,β=60°;
故答案为:30,60;
深入探究:
(2)α与β的关系是β=2(90°﹣α);理由如下:
连接PC,如图3所示:
∵点Q与点P关于点E对称,
∴EP=EQ,
∵CE⊥AP,
∴CE垂直平分PQ,
∴CP=CQ,
∴∠QCE=∠PCE,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,∠ABD=∠CBD=45°,
在△ABP和△CBP中, ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=∠BAD﹣∠DAP=90°﹣α,AP=CP,
∵∠ABG=∠CEG=90°,
∴∠BAP+∠AGB=90°,∠GCE+∠CGE=90°,
∵∠AGB=∠CGE,
∴∠BAP=∠GCE,
∴∠BCG=∠GCE=90°﹣α,
∴∠QCE=2∠GCE=2(90°﹣α),
即:β=2(90°﹣α);
拓展延伸:
(3)①当90°<α<135°时,α与β之间的等量关系为β=2(α﹣90°);理由如下:
连接PC,设CE交AB于点H,如图4所示:
∵点Q与点P关于点E对称,
∴EP=EQ,
∵CE⊥AP,
∴CE垂直平分PQ,
∴CP=CQ,
∴∠PCE=∠QCE=β,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,∠ABD=∠CBD=45°,
∴∠ABP=∠CBP,
在△ABP和△CBP中, ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=∠DAP﹣∠BAD=α﹣90°,
∵∠AEH=∠CBH=90°,
∴∠BAP+∠AHE=90°,∠BCH+∠BHC=90°,
∵∠AHE=∠CHB,
∴∠BAP=∠BCH,
∴∠BCP=∠BCH=∠BAP=α﹣90°,
∴∠QCE=∠PCE=2∠BCP=2(α﹣90°),
即:β=2(α﹣90°);
故答案为:β=2(α﹣90°);
②当0°<α<45°时,β=2α,不合题意;
当45°<α<90°时,β=2(90°﹣α),
∵α=β,
∴α=β=60°,
作PM⊥AD于M,如图5所示:
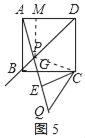
∵∠APM=90°﹣α=30°,∠PDM=45°,
∴AM=![]() AP,DM=PM=
AP,DM=PM=![]() AM,
AM,
设AM=x,则CP=AP=2x,DM=PM=![]() x,
x,
∵AD=2,
∴x+![]() x=2,
x=2,
解得:x=![]() ﹣1,
﹣1,
∴CP=AP=2x=2﹣![]() ,
,
∵∠PCQ=2β=120°,CP=CQ,CE⊥AP,
∴∠CPE=30°,PE=QE,
∴CE=![]() CP=
CP=![]() ﹣1,PE=
﹣1,PE=![]() CE=3﹣
CE=3﹣![]() ,
,
∴PQ=2PE=6﹣2![]() ;
;
当90°<α<135°时,β=2(α﹣90°),
∵α=β,
∴α=β=180°,不合题意;
综上所述,在点P运动过程中,当α=β时,PQ的长为6﹣2![]() ;
;
故答案为:6﹣2![]() .
.