题目内容
【题目】如图，PA、PB分别与⊙O相切于点A、B，若∠P=50°，则∠C的值是（ ）
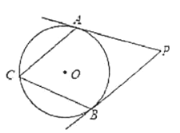
A. 50°B. 55°C. 60°D. 65°
【答案】D
【解析】
连接OA、OB，由已知的PA、PB与圆O分别相切于点A、B，根据切线的性质得到OA⊥AP，OB⊥PB，从而得到∠OAP=∠OBP=90°，然后由已知的∠P的度数，根据四边形的内角和为360°，求出∠AOB的度数，最后根据同弧所对的圆周角等于它所对圆心角度数的一半即可得到∠C的度数．
解：连接OA、OB，
∵PA、PB与圆O分别相切于点A、B，
∴OA⊥AP，OB⊥PB，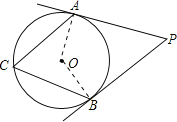
∴∠OAP=∠OBP=90°，又∠P=50°，
∴∠AOB=360°-90°-90°-50°=130°，
又∵∠ACB和∠AOB分别是弧AB所对的圆周角和圆心角，
∴∠C=
∠AOB=×130°=65°．
故选：D．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】己知二次函数y=ax2+bx+c的y与x的部分对应值如下表；
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论：①抛物线的开口向下；②其图象的对称轴为x=1;③当x﹤l时，函数值y随x 的增大而增大；④方程ax2+bx+c=0有一个根大于4.其中正确的结论有（ ）
A. 4个B. 1个C. 3个D. 2个
