题目内容
【题目】己知二次函数y=ax2+bx+c的y与x的部分对应值如下表；
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论：①抛物线的开口向下；②其图象的对称轴为x=1;③当x﹤l时，函数值y随x 的增大而增大；④方程ax2+bx+c=0有一个根大于4.其中正确的结论有（ ）
A. 4个B. 1个C. 3个D. 2个
【答案】D
【解析】
根据二次函数的图象具有对称性和表格中的数据，可以得到对称轴为x=
=
，再由图象中的数据可以得到当x=取得最大值，从而可以得到函数的开口向下以及得到函数当x＜时，y随x的增大而增大，当x＞时，y随x的增大而减小，然后根据x=0时，y=1，x=-1时，y=-3，可以得到方程ax2+bx+c=0的两个根所在的大体位置，从而可以解答本题．
解：由表格可知，
二次函数y=ax2+bx+c有最大值，当x==时，取得最大值，
∴抛物线的开口向下，故①正确，其图象的对称轴是直线x=，故②错误，
当x＜时，y随x的增大而增大，故③正确，
方程ax2+bx+c=0的一个根大于-1，小于0，则方程的另一个根大于2×
=3，小于3+1=4，故④错误，
故选：D．
【题目】小张同学尝试运用课堂上学到的方法，自主研究函数
的图像与性质.下面是小张同学在研究过程中遇到的几个问题，现由你来完成：
（1）函数y=
的定义域是 ；
（2）下表列出了
与
的几组对应值：
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … |
|
|
|
|
| 4 |
| 1 |
|
| … |
表中
的值是 ；
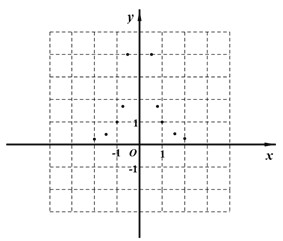
（3）如图，在平面直角坐标系
中，描出以表中各组对应值为坐标的点，试由描出的点画出该函数的图像；
（4）结合函数的图像，写出这个函数的性质： .（只需写一个）
【题目】某市居民使用自来水按如下标准收费（水费按月缴纳）：
户月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
（1）当
时，某用户一个月用了
水，求该用户这个月应缴纳的水费；
（2）设某户月用水量为
立方米，当
时，求该用户应缴纳的水费（用含
、的整式表示）；
（3）当时，甲、乙两用户一个月共用水
.已知甲用户用水量超过了
，设甲用户这个月用水如
的整式表示）
