题目内容
【题目】如图，一次函数
的图象与
轴交于点
，与反比例函数
的图象在第一象限交于点
，过点
作
轴上点
，
的面积为
．
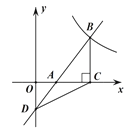
（1）求反比例函数
的解析式；
（2）求证：
是等腰三角形．
【答案】（1）
；（2）证明见解析．
【解析】
（1）先根据点A、B的坐标求出AC的长，再根据三角形的面积公式可求出OD的长，从而可得点D的坐标，然后利用待定系数法可求出一次函数的解析式，从而可得点B的坐标，最后利用待定系数法即可得；
（2）先根据点B的坐标可得BC的长，再根据勾股定理可求出CD的长，从而可得
，然后根据等腰三角形的定义即可得证．
（1）∵点
，点
∴点
坐标为
∴
∴
∴
∴
∴点
坐标为
把
，代入
得：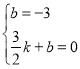
解得
∴直线的解析式为
把点代入得
∴
∴
则反比例函数的解析式为；
（2）∵，
，
∴
，
，
在
中，
∴
∴
是等腰三角形．
阅读快车系列答案
【题目】某水果店以10元/千克的价格购进某种水果进行销售，经过市场调查获得部分数据如下表：
销售价格x（元/千克） | 10 | 13 | 16 | 19 | 22 |
日销售量y（千克） | 100 | 85 | 70 | 55 | 40 |
（1）请根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识刻画y与x之间的函数关系；
（2）该水果店应该如何确定这批水果的销售价格，才能使日销售利润最大？
（3）若该水果店平均每销售1千克这种水果会损耗a千克，当20≤x≤22时，水果店日获利的最大值为405元，求a的值．
【题目】某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件，每件文化衫的批发价及手绘后的零售价如表：
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件？
(2)通过手绘设计后全部售出，求该校这次义卖活动所获利润．
