题目内容
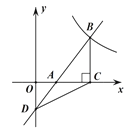
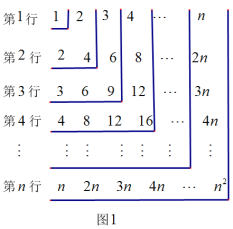
【题目】如图，有一块矩形纸片ABCD，AB=8，AD=6．将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为_____．
【答案】2
【解析】
根据折叠的性质，在图②中得到DB=8﹣6=2，∠EAD=45°；在图③中，得到AB=AD﹣DB=6﹣2=4，△ABF为等腰直角三角形，然后根据等腰三角形的性质和矩形的性质得到BF=AB=4，CF=BC﹣BF=6﹣4=2，EC=DB=2，最后根据三角形的面积公式计算即可．
解：∵AB=8，AD=6，纸片折叠，使得AD边落在AB边上，图②，
∴DB=8﹣6=2，∠EAD=45°，
又∵△AED沿DE向右翻折，AE与BC的交点为F，图③，
∴AB=AD﹣DB=6﹣2=4，△ABF为等腰直角三角形，
∴BF=AB=4，
∴CF=BC﹣BF=6﹣4=2，
而EC=DB=2，
∴△CEF的面积=
×2×2=2．
故答案为2．
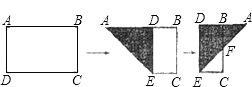
【题目】如图，在△ABC中，AD⊥BC于D，下列条件：（1）∠B+∠DAC＝90°；（2）∠B＝∠DAC；（3）
；（4）AB2＝BDBC．其中一定能够判定△ABC是直角三角形的有（填序号）_____．
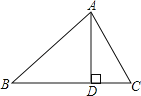
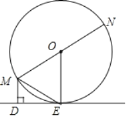
【题目】如图，⊙O的直径AB＝4cm，点C为线段AB上一动点，过点C作AB的垂线交⊙O于点D，E，连结AD，AE．设AC的长为xcm，△ADE的面积为ycm2．
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）确定自变量x的取值范围是 ；
（2）通过取点、画图、测量、分析，得到了y与x的几组对应值，如下表：
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
（3）如图，建立平面直角坐标系xOy，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
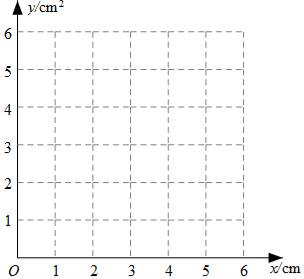
（4）结合画出的函数图象，解决问题：当△ADE的面积为4cm2时，AC的长度约为 cm．
【题目】某公司招聘一名职员，先对应聘者进行笔试考核，笔试进入前两名的选手再进入面试方面的考核，最终在参加面试的两人中录取一人．该公司将应聘者的笔试成绩划分了4个等级：设应聘者的成绩为x（单位：分），当60≤x＜70时为不合格；当70≤x＜80时为合格；当80≤x＜90时为良好；当90≤x≤100时为优秀．下面是参加笔试的10名应聘者的成绩：86 75 67 86 92 75 82 90 86 78
（1）这10名应聘者的笔试成绩的中位数是_______，众数是_______；
（2）请将下面表示上述4个等级的统计图补充完整；
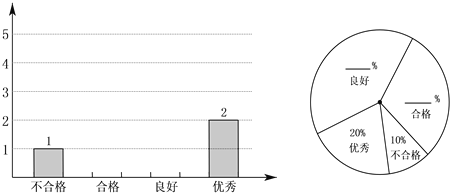
（3）该公司对进入笔试前两名的甲、乙二人进行了面试考核，面试中包括形体、口才、人际交往、创新能力，他们的成绩（百分制）如下表：
候选人 | 面试项目 | |||
形体 | 口才 | 人际交往 | 创新能力 | |
甲 | 86 | 90 | 95 | 90 |
乙 | 95 | 85 | 90 | 92 |
如果公司根据经营性质和岗位要求，以面试成绩中形体占10%，口才占20%，人际交往40%，创新能力占30%确定成绩，那么你认为该公司应该录取谁？请通过计算说明理由．
