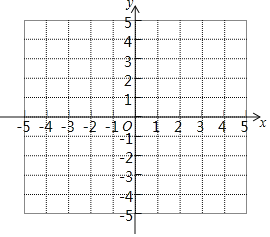��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У��������¶��壺����P��ͼ��M�ϣ���Q��ͼ��N�ϣ����߶�PQ���ȵ���СֵΪͼ��M��N���ܾ࣬��Ϊd��M��N�����ر�أ���ͼ��M��N�й����㣬�涨d��M��N��=0��
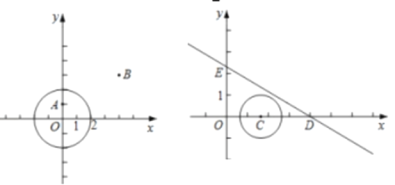
��1����ͼ1����O�İ뾶Ϊ2��
����A��0��1����B��4��3������d��A����O��= ��d��B����O��= ��
����ֱ֪��L��y=![]() ����O���ܾ�d��L����O��=
����O���ܾ�d��L����O��=![]() ����b��ֵ��
����b��ֵ��
��2����ͼ2��CΪx����������һ�㣬��C�İ뾶Ϊ1��ֱ��y=��![]() ��x�ύ�ڵ�D����y�ύ�ڵ�E��ֱ��DE����C���ܾ�d��DE����C��
��x�ύ�ڵ�D����y�ύ�ڵ�E��ֱ��DE����C���ܾ�d��DE����C��![]()
![]() ����ֱ��д��Բ��C�ĺ�����m��ȡֵ��Χ��
����ֱ��д��Բ��C�ĺ�����m��ȡֵ��Χ��
���𰸡���1��d��A����O��= 1 ��d��B����O��= 3 ����2��b=![]() ����3��
����3��![]() .
.
��������
��1��������OB,ֻ�����OA��OB���ɽ�𣻢�����������OK��,�ٸ������⽨������b�ķ��̼��ɽ�����⣻��2���������⣬ȷ��C����x���ϵķ�Χ������������ֵ��ȷ��m�ķ�Χ.
��1������ͼ������OB����B����BH��x�ᣬ����ΪH,
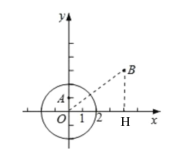
�ߡ�O�İ뾶Ϊ2����A��0��1����
��d��A�� ��O��=2-1=1��
��B(4��3)����OB=5��
��d��B����O��=5-2=3.
����ͼ����ֱ����x��,y�ύP��Q���㣬��O��OK��PQ,����ΪK,
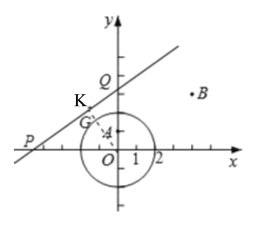
��P��![]() ��0����Q��0��b����
��0����Q��0��b����
��OP=![]() ��OQ=
��OQ=![]() ��
��
�ɹ��ɶ����ã�PQ=![]() ��,
��,
��![]() ��
��
��![]() ��
��
��OK=![]() ��
��
��d��L����O��=![]() ��
��
��![]() -2=
-2=![]() ��
��
��b=��4.
��2����ͼ����CR��ED�ڵ�R��CS��ED�ڵ�S��
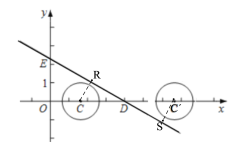
��CR=CS=![]() �����Cλ��C��C֮�䣨����C��C ����
�����Cλ��C��C֮�䣨����C��C ����
��E��0��![]() ����D��4��0����
����D��4��0����
��OE=![]() ��OD=4���ɹ��ɶ����ã�ED=
��OD=4���ɹ��ɶ����ã�ED=![]() ��
��
��sin��CDR=![]() ��
��
��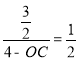 ��
��
��OC=1����OC=7��
��![]() .
.