��Ŀ����
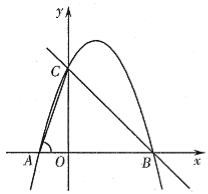
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y=��x+n��x�ᡢy��ֱ���B��C���㣬������y=ax2+bx+3(a��0)��C��B���㣬��x������һ��A������AC����tan��CAO=3��
(1)�������ߵĽ���ʽ��
(2)����P������CB��һ�㣬����P��x��Ĵ��ߣ�����ΪH������������Q����P�������Ϊt���߶�PQ�ij�Ϊd�����d��t֮��ĺ�����ϵʽ����д����Ӧ���Ա���t��ȡֵ��Χ��
(3)��(2)�������£�����P���߶�BC��ʱ����PH=e����֪d��e����yΪδ֪����һԪ���η��̣�y2��(m+3)y+![]() (5m2��2m+13)=0 (mΪ����)������ʵ��������M���������ϣ�����MQ��MH��PM���ң�MPƽ����QMH�����tֵ����M�����꣮
(5m2��2m+13)=0 (mΪ����)������ʵ��������M���������ϣ�����MQ��MH��PM���ң�MPƽ����QMH�����tֵ����M�����꣮
���𰸡�(1) y=-x2+2x+3��(2) 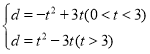 ����3��t=1, (1+
����3��t=1, (1+![]() ��2)��(1��
��2)��(1��![]() ��2).
��2).
��������
�����������1����x=0ʱ����������y=ax2+bx+3��a��0���Ϳ������y=3���ó�C�����꣬�Ϳ��Եó�ֱ�ߵĽ���ʽ���Ϳ������B�����꣬��ֱ��������AOC�У��������κ���ֵ�Ϳ������OA��ֵ���ó�A�����꣬���ɴ���ϵ����������Ԫһ�η�����������Ϳ��Եó����ۣ�
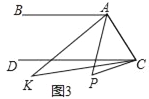
��2��������������ۣ�����P���߶�CB��ʱ������ͼ3��P������BN��ʱ������P�������Ϊ��t��-t+3����Q�������Ϊ��t��-t2+2t+3�����Ϳ��Եó�d��t֮��ĺ�����ϵʽ���ó����ۣ�
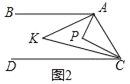
��3�����ݸ����б�ʽ�Ϳ������m��ֵ���Ϳ���������̵Ľ�����PQ��PH��ֵ���ӳ�MP��L��ʹLP=MP������LQ��LH����ͼ2���ӳ�MP��L��ʹLP=MP������LQ��LH���Ϳ��Եó��ı���LQMH��ƽ���ı��Σ������ó��ı���LQMH�����Σ������ε����ʾͿ���������ۣ�
�����������1����x=0����y=-x+n=0+n=n��y=ax2+bx+3=3��
��OC=3=n��
��y=0��
��-x+3=0��x=3=OB��
��B��3��0����
����AOC����AOC��90����tan��CAO=![]() ��
��
��OA=1��
��A��-1��0����
��A��-1��0����B��3��0������y=ax2+bx+3��
��
![]() ��
��
��ã�![]()
�������ߵĽ���ʽ��y=-x2+2x+3��
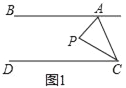
(2) ��ͼ1��
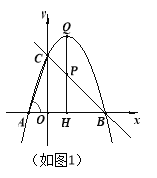
��P��ĺ�����Ϊt ��PQ��ֱ��x�� ��P�������Ϊ(t����t+3)��
Q�������Ϊ(t����t2+2t+3).
��PQ=|(��t+3)��(��t2+2t+3)|=| t2��3t |
��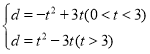 ��
��
��d��e��y2��(m+3)y+![]() (5m2��2m+13)=0��mΪ������������ʵ������
(5m2��2m+13)=0��mΪ������������ʵ������
�����0������=(m+3)2��4��![]() (5m2��2m+13)��0
(5m2��2m+13)��0
�������= ��4(m��1)2��0������4(m��1)2��0��
���=0��m=1��
�� PQ��PH��y2��4y+4=0������ʵ���������![]() y1=y2=2
y1=y2=2
����ʱQ�������ߵĶ��㣬
�ӳ�MP��L��ʹLP=MP������LQ��LH����ͼ2��
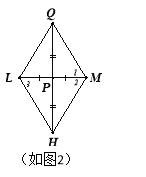
��LP=MP��PQ=PH�����ı���LQMH��ƽ���ı��Σ�
��LH��QM�����1=��3���ߡ�1=��2�����2=��3��
��LH=MH����ƽ���ı���LQMH�����Σ�
��PM��QH������M����������P����������ͬ������2��
����y=��x2+2x+3��y=2����x2��2x��1=0����x1=1+![]() ��x2=1��
��x2=1��![]()
���ϣ�tֵΪ1��M������Ϊ(1+![]() ��2)��(1��
��2)��(1��![]() ��2)
��2)

 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�