题目内容
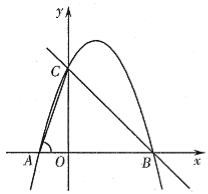
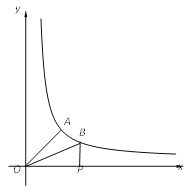
【题目】如图,已知A、B是反比例函数y=![]() 图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=
图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=![]() .
.
(1)求点A的坐标;
(2)连接AB,求四边形AOPB的面积.
【答案】(1)A(2![]() ,2
,2![]() );(2)4+2
);(2)4+2![]()
【解析】试题分析:(1)、过点A作AC⊥OP交OP于点C,根据等腰直角三角形的性质得出AC和OC的长度,从而得到点A的坐标;(2)、根据点A的坐标求出反比例函数解析式,根据∠BOP的正切值设点B的坐标为(2m,m),然后代入函数解析式求出m的值,最后根据四边形AOPB的面积等于四边形ACPB的面积加上△AOC的面积得出答案.
试题解析:(1)、过点A作AC⊥OP交 OP于点C 在Rt△AOC中,∵∠AOP=45°.
∴AC=OC=2![]() ,即A(2
,即A(2![]() ,2
,2![]() )
)
(2)把A(2![]() ,2
,2![]() )代入y=
)代入y= ![]() 得k=8,即y=
得k=8,即y= ![]()
在Rt△OBP中,tan∠BOP=![]() ,即OP=2BP,设BP=m,即B(2m,m)
,即OP=2BP,设BP=m,即B(2m,m)
把B(2m,m)代入y=![]() ,m=2,即BP=2,OP=4
,m=2,即BP=2,OP=4
∴S四边形AOPB=S四边形ACPB+S△CPB=![]() 2
2![]() 2
2![]() +
+![]() (2+2
(2+2![]() )(4-2
)(4-2![]() )=4+2
)=4+2![]()

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目