题目内容
【题目】已知:过⊙O外一点C作⊙O的切线BC,B为切点,AB是直径,AC与⊙O交于D.
(1)若∠AOD=120°,求∠C的度数;
(2)若AD=8,sinC=![]() ,求AB的长.
,求AB的长.
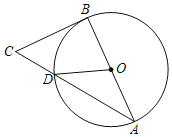
【答案】(1)60°;(2)10.
【解析】
![]() 先利用等腰三角形的性质和三角形内角和计算出
先利用等腰三角形的性质和三角形内角和计算出![]() ,再根据切线的性质得到
,再根据切线的性质得到![]() ,然后利用互余可计算出
,然后利用互余可计算出![]() ;
;
![]() 连接BD,如图,利用圆周角定理得到
连接BD,如图,利用圆周角定理得到![]() ,根据等角的余角相等得到
,根据等角的余角相等得到![]() ,然后利用正弦的定义可计算出AB.
,然后利用正弦的定义可计算出AB.
解:(1)∵OA=OD,
∴∠A=∠ODA=![]() (180°-∠AOD)=
(180°-∠AOD)=![]() (180°-120°)=30°,
(180°-120°)=30°,
∵BC为⊙O的切线,AB是直径,
∴AB⊥BC,
∴∠ABC=90°,
∴∠C=90°-∠A=90°-30°=60°;
(2)连接BD,如图,
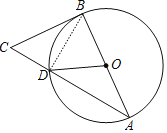
∵AB为直径,
∴∠ADB=90°,
∴∠C+∠A=90°,∠ABD+∠A=90°,
∴∠ABD=∠C,
在Rt△ABD中,sin∠ABD=![]() =
=![]() ,
,
∴AB=![]() ×8=10.
×8=10.

练习册系列答案
相关题目
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收1元印刷费,另收150元的制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.设在同一家印刷厂一次印制数量为![]() 份(
份(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
一次印制数量(份) | 5 | 10 | 20 | … |
|
甲印刷厂收费(元) | 155 | … | |||
乙印刷厂收费(元) | 12.5 | … |
(2)在印刷品数量大于800份的情况下选哪家印刷厂印制省钱?