题目内容
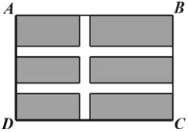
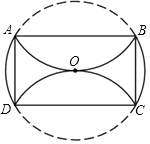
【题目】如图,在⊙O中,分别将![]() 、
、![]() 沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
A.8B.![]() C.32D.
C.32D.![]()
【答案】B
【解析】
过O作OH⊥AB交⊙O于E,延长EO交CD于G,交⊙O于F,连接OA,OB,OD,根据平行线的性质得到EF⊥CD,根据折叠的性质得到OH=![]() OA,进而推出△AOD是等边三角形,得到D,O,B三点共线,且BD为⊙O的直径,求得∠DAB=90°,同理,∠ABC=∠ADC=90°,得到四边形ABCD是矩形,于是得到结论.
OA,进而推出△AOD是等边三角形,得到D,O,B三点共线,且BD为⊙O的直径,求得∠DAB=90°,同理,∠ABC=∠ADC=90°,得到四边形ABCD是矩形,于是得到结论.
过O作OH⊥AB交⊙O于E,延长EO交CD于G,交⊙O于F,连接OA,OB,OD.
∵AB∥CD,∴EF⊥CD.
∵分别将![]() 、
、![]() 沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,∴OH=
沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,∴OH=![]() OA,∴∠HAO=30°,∴∠AOH=60°,同理∠DOG=60°,∴∠AOD=60°,∴△AOD是等边三角形.
OA,∴∠HAO=30°,∴∠AOH=60°,同理∠DOG=60°,∴∠AOD=60°,∴△AOD是等边三角形.
∵OA=OB,∴∠ABO=∠BAO=30°,∴∠AOB=120°,∴∠AOD+∠AOB=180°,∴D,O,B三点共线,且BD为⊙O的直径,∴∠DAB=90°,同理,∠ABC=∠ADC=90°,∴四边形ABCD是矩形,∴AD=AO=4,AB=![]() AD=4
AD=4![]() ,∴四边形ABCD的面积是16
,∴四边形ABCD的面积是16![]() .
.
故选B.


练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 |
|
|
|
|
面试 |
|
|
|
|
(1)这![]() 名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
(2)该公司规定:笔试、面试分别按![]() ,
,![]() 的比例计总分,请比较甲、乙的总分的大小.
的比例计总分,请比较甲、乙的总分的大小.