题目内容
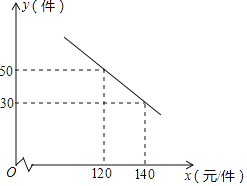
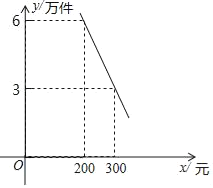
【题目】某公司每月生产产品A4万件和同类新型产品B若干万件.产品A每件销售利润为200元,且在产品B销售量每月不超过3万件时,每月4万件产品A能全部销售,产品B的每月销售量y(万件)与每件销售利润x(元)之间的函数关系图象如图所示.
(1)求y与x的函数关系式;
(2)在保证A产品全部销售的情况下,产品B每件利润定为多少元时公司销售产品A和产品B每月可获得总利润w1(万元)最大?
(3)在不要求产品A全部销售的情况下,已知受产品B销售价的影响产品A每月销售量:(万件)与x(元)之间满足关系z=0.024x﹣3.2,那么产品B每件利润定为多少元时,公司每月可获得最大的利润?并求最大总利润w2(万元).
【答案】(1)y=﹣0.03x+12;(2)产品B的每件利润为300元时,公司每月利润w1最大;(3)产品B每件利润定为280元时,每月可获得最大利润为1712万元.
【解析】
(1)设y=kx+b,从图象中可知函数经过点(200,6),(300,3),代入即可;
(2)w1=﹣0.03(x﹣200)2+2000,当x=300时,w1有最大值;
(3)w2=﹣0.03(x﹣280)2+1712,当x=280时,w2最大值为1712万元.
解:(1)设y=kx+b,从图象中可知函数经过点(200,6),(300,3),
∴![]() ,
,
∴![]() ,
,
∴y=﹣0.03x+12;
(2)由题意得:
w1=4×200+(﹣0.03x+12)x=﹣0.03x2+12x+800=﹣0.03(x﹣200)2+2000,
∵y≤3,﹣0.03x+12≤3,
∴x≥300,
∵x≥200时,w1随x的增大而减小,
∴当x=300时,w1有最大值,
∴产品B的每件利润为300元时,公司每月利润w1最大;
(3)w2=200×(0.024x﹣3.2)+(﹣0.03x+12)x=﹣0.03x2+16.8x﹣640=﹣0.03(x﹣280)2+1712,
当x=280时,w2最大值为1712万元,
∴产品B每件利润定为280元时,每月可获得最大利润为1712万元.

 阅读快车系列答案
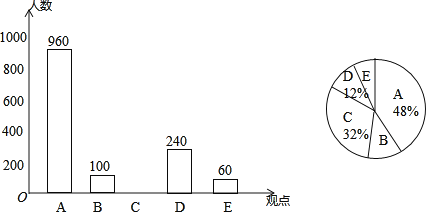
阅读快车系列答案【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.