Question

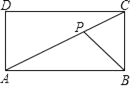
【题目】如图，点P是矩形ABCD的对角线AC上的一点（异于两个端点），AB＝2BC＝2，若BP的垂直平分线EF经过该矩形的一个顶点，则BP的垂直平分线EF与对角线AC的夹角（锐角）的正切值为_____．

Answer 1

【答案】或2﹣2

【解析】

分两种情况：①当BP的垂直平分线经过顶点C时，连接PE，则PC＝BC＝1，PE＝BE,△PCE≌△BCE，得出∠APE＝∠CPE＝∠ABC＝90°，由勾股定理求出AC＝＝，的AP＝﹣1，证明△APE∽△ABC，求出PE＝，即可得出tan∠ACE的值；

②当BP的垂直平分线经过顶点A时，连接PE，则AP＝AB＝2，PE＝BE，△APE≌△ABE，的∠APE＝∠CPE＝∠ABC＝90°，PC＝AC﹣AP＝﹣2，

同①得：△CPE∽△CBA，求出PE＝＝2﹣4，求出tan∠CAE的值即可．

∵AB＝2BC＝2，

∴BC＝1，

分两种情况：

①当BP的垂直平分线经过顶点C时，如图1所示：连接PE，

则PC＝BC＝1，PE＝BE，△PCE≌△BCE，

∴∠APE＝∠CPE＝∠ABC＝90°，

∵AC＝＝，

∴AP＝﹣1，

∵∠PAE＝∠BAC，

∴△APE∽△ABC，

∴，

∴PE＝，

∴tan∠ACE＝＝；

②当BP的垂直平分线经过顶点A时，如图2所示：连接PE，

则AP＝AB＝2，PE＝BE，△APE≌△ABE，

∴∠APE＝∠CPE＝∠ABC＝90°，

∴PC＝AC﹣AP＝﹣2，

同①得：△CPE∽△CBA，

∴，

∴PE＝，

∴tan∠CAE＝；

综上所述，BP的垂直平分线EF与对角线AC的夹角（锐角）的正切值为或2﹣2；