Question

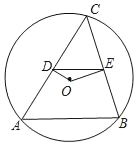
【题目】如图1，⊙O的直径AB＝12，P是弦BC上一动点（与点B，C不重合），∠ABC＝30°，过点P作PD⊥OP交⊙O于点D．

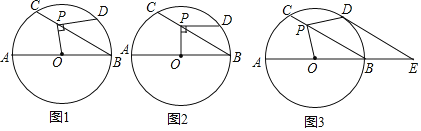
（1）如图2，当PD∥AB时，求PD的长；

（2）如图3，当时，延长AB至点E，使BE＝AB，连接DE．

①求证：DE是⊙O的切线；

②求PC的长．

Answer 1

【答案】（1）2；（2）①见解析；②CP的长为：3﹣3或3+3．

【解析】

（1）根据题意首先得出半径长，再利用锐角三角函数关系得出OP，PD的长；
（2）①首先得出△OBD是等边三角形，进而得出∠ODE=∠OFB=90°，求出答案即可；
②首先求出CF的长，进而利用直角三角形的性质得出PF的长，进而得出答案．

解：（1）如图2，连接OD，

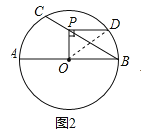
∵OP⊥PD，PD∥AB，

∴∠POB＝90°，

∵⊙O的直径AB＝12，

∴OB＝OD＝6，

在Rt△POB中，∠ABC＝30°，

∴OP＝OBtan30°＝6×＝2，

在Rt△POD中，

PD＝＝＝2；

（2）①证明：如图3，连接OD，交CB于点F，连接BD，

∵，

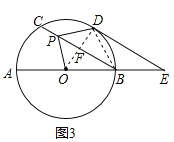
∴∠DBC＝∠ABC＝30°，

∴∠ABD＝60°，

∵OB＝OD，

∴△OBD是等边三角形，

∴OD⊥FB，

∵BE＝AB，

∴OB＝BE，

∴BF∥ED，

∴∠ODE＝∠OFB＝90°，

∴DE是⊙O的切线；

②由①知，OD⊥BC，

∴CF＝FB＝OBcos30°＝6×＝3，

在Rt△POD中，OF＝DF，

∴PF＝DO＝3（直角三角形斜边上的中线，等于斜边的一半），

∴CP＝CF﹣PF＝3﹣3，

当点P在点B与点F之间时，同理可得：

CP＝CF+PF＝3+3，

综上所述：CP的长为：3﹣3或3+3．