题目内容
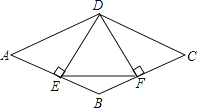
【题目】在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
(1)若点P落在矩形ABCD的边AB上(如图1).
①当点P与点A重合时,∠DEF= °,当点E与点A重合时,∠DEF= °.
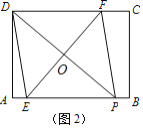
②当点E在AB上时,点F在DC上时(如图2),若AP=![]() ,求四边形EPFD的周长.
,求四边形EPFD的周长.
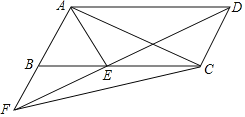
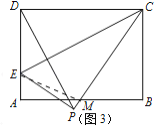
(2)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图3),当AM=DE时,请求出线段AE的长度.
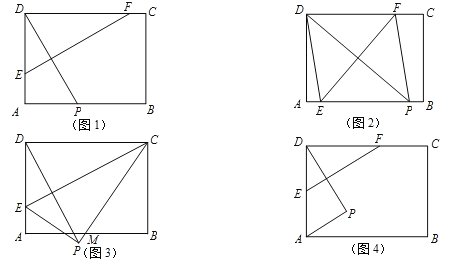
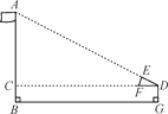
(3)若点P落在矩形的内部(如图4),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
【答案】(1)①90,45;②![]() ;(2)
;(2)![]() 0.6;(3)1.
0.6;(3)1.
【解析】
(1)①当点![]() 与点
与点![]() 重合时,
重合时,![]() 是
是![]() 的中垂线,可得结论;当点
的中垂线,可得结论;当点![]() 与点
与点![]() 重合时,如图2,则
重合时,如图2,则![]() 平分
平分![]() ;
;
②如图3中,证明![]() 得
得![]() ,根据一组对边平行且相等得:四边形
,根据一组对边平行且相等得:四边形![]() 是平行四边形,加上对角线互相垂直可得
是平行四边形,加上对角线互相垂直可得![]() 为菱形,当
为菱形,当![]() 时,设菱形的边长为
时,设菱形的边长为![]() ,根据勾股定理列方程得:
,根据勾股定理列方程得:![]() ,求出
,求出![]() 的值即可;
的值即可;
(2)连接![]() ,由折叠性质可证
,由折叠性质可证![]() ,设
,设![]() .根据全等性质用x表示出线段关系,再由
.根据全等性质用x表示出线段关系,再由![]() 中
中![]() 可列方程求解;
可列方程求解;
(3)如图![]() ,当
,当![]() 与
与![]() 重合,点
重合,点![]() 在对角线
在对角线![]() 上时,
上时,![]() 有最小值,根据折叠的性质求
有最小值,根据折叠的性质求![]() ,由勾股定理求
,由勾股定理求![]() ,所以
,所以![]() .
.
解:(1)①当点![]() 与点
与点![]() 重合时,
重合时,
![]() 是
是![]() 的中垂线,
的中垂线,
![]() ,
,
当点![]() 与点
与点![]() 重合时,
重合时,
此时![]() ,
,
故答案为:90,45.
②如图2中,设![]() 与
与![]() 交于点
交于点![]() ,由折叠知
,由折叠知![]() 垂直平分
垂直平分![]() .
.
![]() ,
,![]() ,
,
![]() 矩形
矩形![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 四边形
四边形![]() 是菱形,
是菱形,
当![]() 时,设菱形边长为
时,设菱形边长为![]() ,则
,则![]() ,
,![]()
在![]() 中,
中,![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]() 菱形的周长
菱形的周长![]() .
.
(2)如图3中,连接![]() ,设
,设![]() .
.
由折叠知![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]()
![]()
解得![]() .
.
![]() .
.
(3)如图![]() 中,连接
中,连接![]() ,
,![]() ,
,![]() .
.

![]() ,
,![]() ,
,
![]() ,此时
,此时![]() 的最小值
的最小值![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 与
与![]() 重合时,
重合时,![]() 的值最小,由折叠得:
的值最小,由折叠得:![]() ,
,

由勾股定理得:![]() ,
,
![]() ,
,
![]() 当
当![]() ,
,![]() ,
,![]() 共线时,
共线时,![]() 有最小值,
有最小值,
![]() ,
,
则![]() 的最小值是1.
的最小值是1.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目