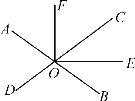
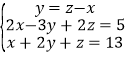题目内容
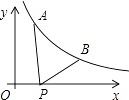
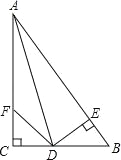
【题目】如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接DF.
(1)求证:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长;
(3)若CF=BE,直接写出线段AB,AF,EB的数量关系:_____.
【答案】解:(1)∵∠C=90°,DE⊥AB
∴∠C=∠AED=90°
在△ACD和△AED中,
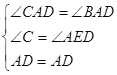
∴△ACD≌△AED
∴AC=AE
(2)由(1)得:△ACD≌△AED
∴DC=DE
∵![]() ,
,
∴![]()
又∵AC="8,AB=10," 且△ABC的面积等于24
∴![]()
∴DE=![]()
(3)AB="AF+2EB"
【解析】
试题(1)根据已知条件利用AAS即可证得△ACD≌△AED,根据全等三角形的对应边相等即可得出结论;(2)根据△ACB的面积=△ACD的面积+△ADB的面积,列式计算即可求出DE的长;(3)
根据题意即可得出:AB=AF+2EB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共人, ![]() ,
, ![]() ;
;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有人.