题目内容
【题目】已知矩形的周长为60．
（1）当该矩形的面积为200时，求它的边长；
（2）请表示出这个矩形的面积与其一边长的关系，并求出当矩形面积取得最大值时，矩形的边长．
【答案】（1）矩形的边长为10和20；（2）这个矩形的面积S与其一边长x的关系式是S=-x2+30x；当矩形的面积取得最大值时，矩形是边长为15的正方形．
【解析】
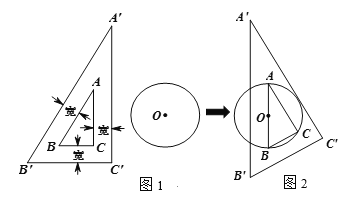
（1）设矩形的一边长为
，则矩形的另一边长为
，根据矩形的面积为200列出相应的方程，从而可以求得矩形的边长；
（2）根据题意可以得到矩形的面积与一边长的函数关系，然后根据二次函数的性质可以求得矩形的最大面积，并求出矩形面积最大时它的边长．
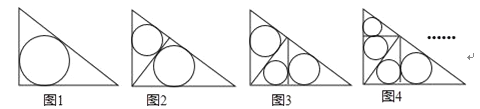
解：（1）设矩形的一边长为，则矩形的另一边长为，根据题意，得
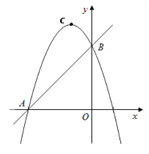
，解得
，
．
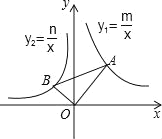
答：矩形的边长为10和20．
（2）设矩形的一边长为，面积为S，根据题意可得，
，
所以，当矩形的面积最大时，
．
答：这个矩形的面积与其一边长的关系式是S=-x2+30x，当矩形面积取得最大值时，矩形是边长为15的正方形．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
