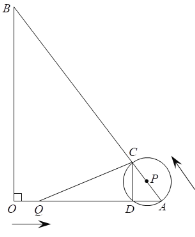
题目内容
【题目】已知在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,
,![]() 是第一象限内任意一点,连接
是第一象限内任意一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() 就叫做点
就叫做点![]() 的“双角坐标”.例如:点
的“双角坐标”.例如:点![]() 的“双角坐标”为
的“双角坐标”为![]() .若点
.若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,则
,则![]() 的最小值为___.
的最小值为___.
【答案】![]()
【解析】
先根据三角形的内角和定理将所求问题转为求![]() 的最大值,再取线段OA的中点B,以B为圆心,OB长为半径画圆,如图(见解析),然后利用圆周角定理和三角形的外角性质即可得.
的最大值,再取线段OA的中点B,以B为圆心,OB长为半径画圆,如图(见解析),然后利用圆周角定理和三角形的外角性质即可得.
由三角形的内角和定理得:![]()
则可将所求问题转为求![]() 的最大值
的最大值
由题意得,点P在直线![]() 位于第一象限的图象上
位于第一象限的图象上
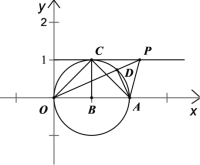
如图,取线段OA的中点B,以B为圆心,OB长为半径画圆
则圆B与直线![]() 相切,设切点为点C
相切,设切点为点C
连接OC、AC、OP、AP,OP与圆B交于点D,连接AD
由圆周角定理可知,![]()
由三角形的外角性质可知,![]() ,即
,即![]()
![]()
因此,![]() ,当且仅当点P与点C重合,等号成立
,当且仅当点P与点C重合,等号成立
即![]() 的最大值为
的最大值为![]()
则![]() 的最小值为
的最小值为![]()
故答案为:![]() .
.

练习册系列答案
相关题目