题目内容
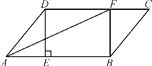
【题目】如图，已知双曲线
经过直角三角形OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为3，则k值是（ ）
A. 3 B. 2 C. 4 D. 
【答案】B
【解析】
过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=
|k|．
如图，过D点作DE⊥x轴，垂足为E．
Rt△OAB中，∵∠OAB=90°，∴DE∥AB．
∵D为Rt△OAB斜边OB的中点D，∴DE为Rt△OAB的中位线．
∵△OED∽△OAB，∴
=．
∵双曲线的解析式是
，∴S△AOC=S△DOE=k，∴S△AOB=4S△DOE=2k，由S△AOB﹣S△AOC=S△OBC=3，得：2k﹣k=3，解得：k=2．
故选B．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
