��Ŀ����
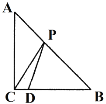
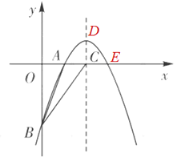
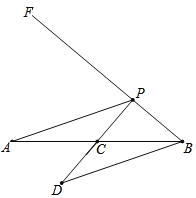
����Ŀ����ͼ����֪�߶�AB��6cm������B������BF�������ABF��40������CΪ�߶�AB�е㣬��PΪ����BF�ϵĶ��㣬����PA������B��PA��ƽ���߽�����PC�ڵ�D����PB�ij���Ϊxcm��PD�ij���Ϊy1cm��BD�ij���Ϊy2cm��������P���B�غ�ʱ��y1��y2��ֵ��Ϊ6cm��
С�ڸ���ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С�ڵ�̽�����̣��벹��������
��1�������±����Ա���x ��0��x��6����ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.0 | 4.7 | 3.9 | 4.1 | 5.1 | 6.6 | 8.4 |
y2/cm | 6.0 | 5.3 | 4.7 | 4.2 | 3.9 | 4.1 |
��˵������ȫ����ʱ�����ֵ����һλС����
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2����������y1��y2��ͼ��
��3����Ϻ���ͼ�������⣺����PDBΪ����������ʱ����BP�ij���ԼΪ�� ��cm��
��4����x��6ʱ���Ƿ����x��ֵʹ����PDBΪ������������ ��������������������������
���𰸡���1��y2��3.9����2������������3��3.1��3.9����4�������ɼ�����
��������
��1����ͼ���������ɵã�
��2�������⣨1���������ݣ���ͬһƽ��ֱ������ϵ![]() �У�����㣬��˳�����Ӹ��㼴�ɣ�
�У�����㣬��˳�����Ӹ��㼴�ɣ�
��3������⣨2����ͼ��![]() ��
��![]() ��
��![]() ����������ۼ��ɵã�
����������ۼ��ɵã�
��4������⣨2����ͼ������![]() ʱ��
ʱ��![]() ��ͼ��
��ͼ��![]() ��ͼ��ֱ��
��ͼ��ֱ��![]() �����Ƿ��н��㼴�ɵó���.
�����Ƿ��н��㼴�ɵó���.
��1���ɻ�ͼ�������ɵã�![]() ʱ��
ʱ��![]() ��
��
��2�������⣨1���������ݣ���ͬһƽ��ֱ������ϵ![]() �У�����㣬��˳�����Ӹ��㣬�õ���ͼ������ͼ��ʾ��
�У�����㣬��˳�����Ӹ��㣬�õ���ͼ������ͼ��ʾ��

��3����![]() ��
��![]() �Ľ���ĺ������֪��
�Ľ���ĺ������֪��![]() ʱ��
ʱ��![]() ����
����![]() ����ʱ
����ʱ![]() Ϊ����������
����������
��ֱ��![]() ��
��![]() �Ľ���ĺ������֪��
�Ľ���ĺ������֪��![]() ʱ��
ʱ��![]() ����
����![]() ����ʱ
����ʱ![]() Ϊ����������
����������
�۲�ͼ���֪��PB�����ܵ���PD
�ʴ�Ϊ3.1��3.9��
��4���۲�ͼ���֪����![]() ʱ��
ʱ��![]() ��ͼ��
��ͼ��![]() ��ͼ��ֱ��
��ͼ��ֱ��![]() ����û�н���
����û�н���
��![]() ����������������
����������������
�ʴ�Ϊ����.

����Ŀ��Ϊ���˽�ѧ��ÿ�µ�����Ǯ������Ӽס��ҡ�������ѧУ�������ȡ200��ѧ�������������ǵ�����Ǯ�������λ��Ԫ������������£�
ѧУƵ������Ǯ | 100��x��200 | 200��x��300 | 300��x��400 | 400��x��500 | 500���� | �ϼ� |
�� | 5 | 35 | 150 | 8 | 2 | 200 |
�� | 16 | 54 | 68 | 52 | 10 | 200 |
�� | 0 | 10 | 40 | 70 | 80 | 200 |
�ڵ�������У���__����������������������������У�����ȡѧ�����鵽��ѧ��������Ǯ������300Ԫ���Ŀ��������