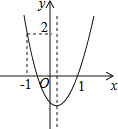题目内容
【题目】关于x的一元二次方程a（x﹣h+1）2+k+2＝0（a＞0）的解是x1＝﹣5，x2＝1，则不等式a（x+h﹣2）2+k＜﹣2的解集为_____．
【答案】0＜x＜6
【解析】
依题意：设y1＝a(x﹣h+1)2+k+2，则抛物线y1与x轴的交点横坐标分别为﹣5，1，设y2＝a(x+h﹣2)2+k+2，则y1与y2关于直线x＝
对称，即可求解．
解：依题意：设y1＝a(x﹣h+1)2+k+2，
则抛物线y1与x轴的交点横坐标分别为﹣5，1，
设y2＝a(x+h﹣2)2+k+2，
∵
,y1与y2的纵坐标相同，
∴y1与y2关于直线x＝对称，
∴抛物线y2与x轴的交点横坐标分别为6，0，
∵a＞0，
∴抛物线y2的开口向上，
∵y2＜0，
∴0＜x＜6，
故答案为：0＜x＜6．
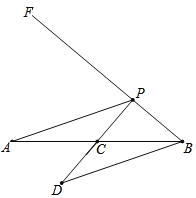
【题目】如图，已知线段AB＝6cm，过点B做射线BF且满足∠ABF＝40°，点C为线段AB中点，点P为射线BF上的动点，连接PA，过点B作PA的平行线交射线PC于点D，设PB的长度为xcm，PD的长度为y1cm，BD的长度为y2cm．（当点P与点B重合时，y1与y2的值均为6cm）
小腾根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．
下面是小腾的探究过程，请补充完整：
（1）按照下表中自变量x （0≤x≤6）的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.0 | 4.7 | 3.9 | 4.1 | 5.1 | 6.6 | 8.4 |
y2/cm | 6.0 | 5.3 | 4.7 | 4.2 | 3.9 | 4.1 |
（说明：补全表格时相关数值保留一位小数）
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出y1，y2的图象；
（3）结合函数图象解决问题：当△PDB为等腰三角形时，则BP的长度约为 cm；
（4）当x＞6时，是否存在x的值使得△PDB为等腰三角形 （填“是”或者“否”）．
