Question

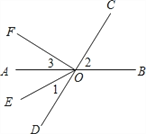
【题目】如图，直线 AB，CD 相交于点O，OE 平分∠AOD，OF⊥OC．

（1）图中∠AOF 的余角是 （把符合条件的角都填出来）；

（2）如果∠AOC=130°36′，那么根据 ，可得∠BOD= °；

（3）如果∠1与∠3的度数之比为3:4，求∠EOC和∠2的度数．

Answer 1

【答案】（1）∠AOD，∠COB；（2）对顶角相等，130.6°；（3）∠EOC=153°，∠2=54°

【解析】试题分析：（1）根据余角定义即可得出结论；

（2）根据对顶角相等得出结论；

（3）设一份为x，表示出∠1和∠3，由邻补角的定义得出∠EOC的度数，由角平分线定义及对顶角的性质得出∠2的度数．

试题解析：解：（1）∵OF⊥OC，∴∠AOF+∠COB=90°，∠AOF+∠AOD=90°，∴∠AOF的余角是∠AOD和∠COB；

（2）∵∠AOC=130°36′=130.6°，∴∠BOD=130.6°（对顶角相等）；

（3）设∠1=3x，则∠3=4x，∵OE 平分∠AOD，∴∠AOE=∠DOE=3x，∵∠FOD=90°，∴3x+3x+4x=90°，∴x=9°，∴∠EOD=3x=27°，∴∠EOC=180°－∠EOD=180°－27°=153°．∵∠EOD=3x=27°，∠2=∠AOD=2∠EOD=2×27°=54°．