题目内容
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF. 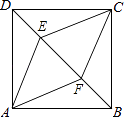
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
【答案】
(1)解:四边形AECF是菱形,理由如下:
连接AC,交BD于点O,
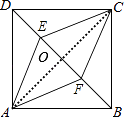
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD
∴DE=BF
∴OE=OF
∴四边形AECF是菱形
(2)解:∵EF=4,DE=BF=2,
∴AC=BD=8,
∴AE= ![]() ,
,
∴四边形AECF的周长为8 ![]()
【解析】(1)连接AC,交BD于点O.利用正方形的性质得出AC⊥BD,OA=OC=OB=OD,进一步得出OE=OF,证得四边形AECF是菱形;(2)利用菱形的性质和勾股定理求得即可.
【考点精析】利用勾股定理的概念和菱形的判定方法对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
相关题目