题目内容
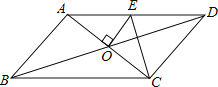
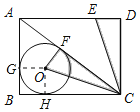
【题目】如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,点E是边AD上一点,连结CE,将△CDE绕点C旋转,当CD落到对角线AC上时,点E恰与圆心O重合,已知AE=6,则下列结论不正确的是( )

A. BC+DE=ACB. ⊙O 的半径是2
C. ∠ACB=2∠DCED. AE=CE
【答案】D
【解析】
⊙O是△ABC的内切圆,设半径为r,切点分别为F、G、H,连接OG、OH,则四边形BGOH是正方形,得出OG=OG=BG=BH=r,由旋转的性质得:OF=DE=r,CF=CD,∠FCO=∠DCE,得出∠ACB=2∠DCE,在Rt△ABC中,由勾股定理得出方程,解方程得出r=2,BC=8,AC=10,选项A、B、C正确;由勾股定理得:CE=![]() ,选项D不正确.
,选项D不正确.
解:⊙O是△ABC的内切圆,设半径为r,切点分别为F、G、H,连接OG、OH,如图:
则四边形BGOH是正方形,
∴OG=OG=BG=BH=r,
由旋转的性质得:OF=DE=r,CF=CD,∠FCO=∠DCE,
∴∠ACB=2∠DCE,
∵BC=AD,
∴AB=CD=CF=AE=6,
由切线长定理得:CH=CF=CD=6,∠ACO=∠BCO,AF=AG=6﹣r,
∴AC=AF+CF=12﹣r,
在Rt△ABC中,由勾股定理得:62+(6+r)2=(12﹣r)2,
解得:r=2,∴BC=8,AC=10,
∴BC+DE=AC,⊙O 的半径是2,
所以选项A、B、C正确;
由勾股定理得:![]() ,选项D不正确;
,选项D不正确;
故选:D.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目