Question

【题目】已知抛物线y=﹣x2+2nx﹣n2+n的顶点为P，直线y=分别交x，y轴于点M，N．

（1）若点P在直线MN上，求n的值；

（2）是否存在过（0，﹣2）的直线与抛物线交于A，B两点（A点在B点的下方），使AB为定长，若存在，求出AB的长；若不存在，请说明理由；

（3）在（2）的条件下，当四边形MABN的周长最小时，求n的值．

Answer 1

【答案】(1) n=;(2) 存在直线y=x﹣2，使AB为定长，且AB=;(3) n=1

【解析】

（1）利用配方法求出顶点P的坐标，利用待定系数法即可解决问题；

（2）设过（0，﹣2）的直线为y=kx﹣2，设A（x1，y1），B（x2，y2），利用k，n表示线段AB，构建方程求出k即可解决问题；

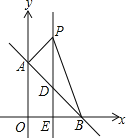
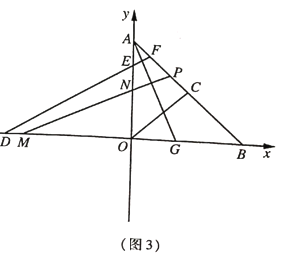
（3）由题意：M（﹣3，0），N（0，），如图，平移AB，使A点于M点重合，则B的对应点G刚好落在y轴上，且G（0，3）．作点G关于直线y=x﹣2的对称点H（5，﹣2）．连接NH交直线y=x﹣2为点R（2，0）．可证明当点B与R重合时，四边形MABN的周长最小．利用待定系数法即可解决问题．

（1）∵y=﹣x2+2nx﹣n2+n=﹣（x﹣n）2+n，∴顶点P（n，n），把P（n，n）代入，得n=．

（2）设过（0，﹣2）的直线为y=kx﹣2，设A（x1，y1），B（x2，y2）．

联立，消元得x2+（k﹣2n）x+n2﹣n﹣2=0，∴，∴，∴y1﹣y2=k（x1﹣x2），∴（y1﹣y2）2=k2（x1﹣x2）2，∴AB2=（x1﹣x2）2+（y1﹣y2）2=（1+k2）[k2+8+（4﹣4k）n]．

∵要使AB为定长，则AB2的值与n的取值无关，∴4﹣4k=0，∴k=1，∴存在直线y=x﹣2，使AB为定长，且AB=．

（3）由题意：M（﹣3，0），N（0，），如图，平移AB，使A点于M点重合，则B的对应点G刚好落在y轴上，且G（0，3）．作点G关于直线y=x﹣2的对称点H（5，﹣2）．

连接NH交直线y=x﹣2为点R（2，0）．

可证明当点B与R重合时，四边形MABN的周长最小．

将 R（2，0）代入y=﹣（x﹣n）2+n中，得：n1=1，n2=4（舍去），∴n=1．