题目内容
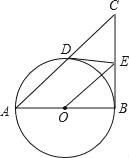
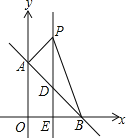
【题目】如图，平面直角坐标系中，直线AB：y＝﹣x+b交y轴于点A（0，4），交x轴于点B．
（1）求直线AB的表达式和点B的坐标；
（2）直线l垂直平分OB交AB于点D，交x轴于点E，点P是直线l上一动点，且在点D的上方，设点P的纵坐标为n．
①用含n的代数式表示△ABP的面积；
②当S△ABP＝8时，求点P的坐标；
③在②的条件下，以PB为斜边在第一象限作等腰直角△PBC，求点C的坐标．
【答案】（1）y＝﹣x+4，点B的坐标为（4，0）；（2）①2n﹣4；②（2，6）；③6，4）．
【解析】
（1）把点A的坐标代入直线解析式可求得b＝4，则直线的解析式为y＝﹣x+4，令y＝0可求得x＝4，故此可求得点B的坐标；
（2）①由题l垂直平分OB可知OE＝BE＝2，将x＝2代入直线AB的解析式可求得点D的坐标，设点P的坐标为（2，n），然后依据S△APB＝S△APD+S△BPD可得到△APB的面积与n的函数关系式为S△APB＝2n﹣4；
②由S△ABP＝8得到关于n的方程可求得n的值，从而得到点P的坐标；
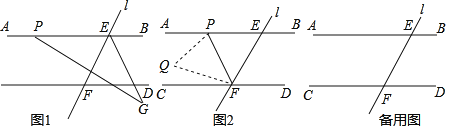
③如图1所示，过点C作CM⊥l，垂足为M，再过点B作BN⊥CM于点N．设点C的坐标为（p，q），先证明△PCM≌△CBN，得到CM＝BN，PM＝CN，然后由CM＝BN，PM＝CN列出关于p、q的方程组可求得p、q的值；如图2所示，同理可求得点C的坐标．
（1）∵把A（0，4）代入y＝﹣x+b得b＝4
∴直线AB的函数表达式为：y＝﹣x+4．
令y＝0得：﹣x+4＝0，解得：x＝4
∴点B的坐标为（4，0）．
（2）①∵l垂直平分OB，
∴OE＝BE＝2．
∵将x＝2代入y＝﹣x+4得：y＝﹣2+4＝2．
∴点D的坐标为（2，2）．
∵点P的坐标为（2，n），
∴PD＝n﹣2．
∵S△APB＝S△APD+S△BPD，
∴S△ABP＝
PDOE+PDBE＝（n﹣2）×2+（n﹣2）×2＝2n﹣4．
②∵S△ABP＝8，
∴2n﹣4＝8，解得：n＝6．
∴点P的坐标为（2，6）．
③如图1所示：过点C作CM⊥l，垂足为M，再过点B作BN⊥CM于点N．
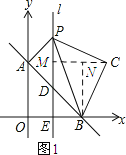
设点C（p，q）．
∵△PBC为等腰直角三角形，PB为斜边，
∴PC＝CB，∠PCM+∠MCB＝90°．
∵CM⊥l，BN⊥CM，
∴∠PMC＝∠BNC＝90°，∠MPC+∠PCM＝90°．
∴∠MPC＝∠NCB．
在△PCM和△CBN中，
，
∴△PCM≌△CBN．
∴CM＝BN，PM＝CN．
∴
，解得
．
∴点C的坐标为（6，4）．
如图2所示：过点C作CM⊥l，垂足为M，再过点B作BN⊥CM于点N．
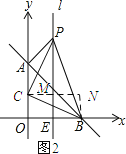
设点C（p，q）．
∵△PBC为等腰直角三角形，PB为斜边，
∴PC＝CB，∠PCM+∠MCB＝90°．
∵CM⊥l，BN⊥CM，
∴∠PMC＝∠BNC＝90°，∠MPC+∠PCM＝90°．
∴∠MPC＝∠NCB．
在△PCM和△CBN中，
，
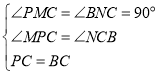∴△PCM≌△CBN．
∴CM＝BN，PM＝CN．
∴
，解得
．
∴点C的坐标为（0，2）舍去．
综上所述点C的坐标为（6，4）．
