题目内容
【题目】已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接BP,CP
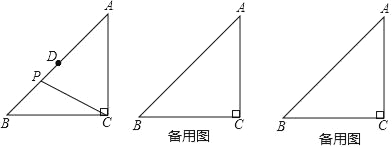
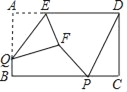
(1)如图,当点P在线段BD上时,求CP的长;
(2)当△BPC是等腰三角形时,求CP的长;
(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.
【答案】(1)PC=3;(2)![]() 或
或![]() ;(3)4+
;(3)4+![]() .
.
【解析】
![]() 如图1中,连接CD.D是AB的中点,可求出CD,再根据勾股定理求出PC;
如图1中,连接CD.D是AB的中点,可求出CD,再根据勾股定理求出PC;
![]() 当△BPC是等腰三角形时,分三种情形讨论;
当△BPC是等腰三角形时,分三种情形讨论;
![]()
![]() 推出点P落在CD的延长线与⊙D的交点处,PC的值最大,推出
推出点P落在CD的延长线与⊙D的交点处,PC的值最大,推出![]() 可得AB′的最大值为
可得AB′的最大值为![]() .
.
(1)如图1中,连接CD.
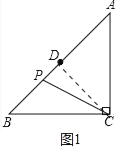
在Rt△ABC中,∠ACB=90°,AC=BC=4,
∴AB=![]() ,
,
∵AD=DB,
∴CD=![]() AB=
AB=![]() ,CD⊥AB,
,CD⊥AB,
在![]() 中,
中,![]()
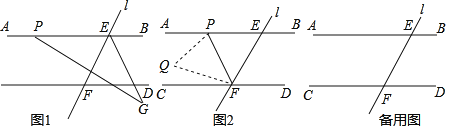
(2)如图2中,
![]()
∴点P在以点D为圆心的⊙D上.
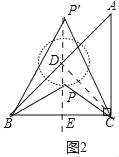
①当PB=PC时,
∵CD=DB,
∴P、D都在线段BC的垂直平分线上,设直线DP交BC于E.
∴∠PEC=90°,BE=CE=2,
∵∠CDB=90°,
∴DE=![]() BC=CE=2,
BC=CE=2,
在![]() 中,
中,![]()
当P在线段PD上时,PE=DE﹣DP=1,![]()
当P在线段ED的延长线上时,PE=ED+DP=3,![]()
②当PC=BC时,![]()
∴PC≠BC,此种情形不存在;
③当PB=BC时,同理这种情形不存在;
如图3中
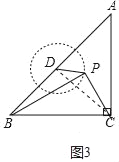
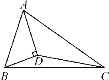
(3)如图4中,连接BB′.
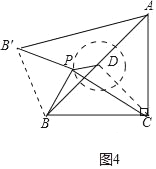
由旋转可知:PB=PB′,∠BPB′=90°,
∴∠PBB′=45°,
∴BB′=![]() PB,
PB,
∴![]()
∵AC=BC,∠ACB=90°,
∴∠ABC=45°,
∴∠ABC=∠PBB′,
∴∠ABB′=∠CBP,
∵![]()
∴![]()
∴![]()
∴△ABB′∽△CBP,
∴![]()
![]()
∴点P落在CD的延长线与⊙D的交点处,PC的值最大,
![]()
∴AB′的最大值为4+![]() .
.

练习册系列答案
相关题目