题目内容
【题目】如图,E,F分别是 □ABCD的边AB,CD的中点,则图中平行四边形的个数共有( ).
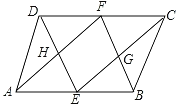
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
首先根据四边形ABCD是平行四边形,可得DC∥AB,DC=AB,再根据E、F分别是边AB、CD的中点,可得DF=FC=![]() DC,AE=EB=
DC,AE=EB=![]() AB,进而可根据一组对边平行且相等的四边形是平行四边形证明四边形DFBE和CFAE都是平行四边形,再根据平行四边形的性质可得DE∥FB,AF∥CE,进而可证出四边形FHEG是平行四边形。
AB,进而可根据一组对边平行且相等的四边形是平行四边形证明四边形DFBE和CFAE都是平行四边形,再根据平行四边形的性质可得DE∥FB,AF∥CE,进而可证出四边形FHEG是平行四边形。
解:∵四边形ABCD是平行四边形,
 ∴DC∥AB,DC=AB,
∴DC∥AB,DC=AB,
∵E、F分别是边AB、CD的中点,
∴DF=FC=![]() DC,AE=EB=
DC,AE=EB=![]() AB,
AB,
∵DC=AB,
∴DF=FC=AE=EB,
∴四边形DFBE和CFAE都是平行四边形,
∴DE∥FB,AF∥CE,
∴四边形FHEG是平行四边形,
故选C。

练习册系列答案
相关题目