��Ŀ����
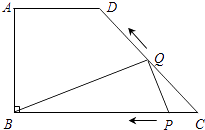
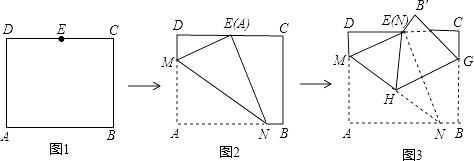
����Ŀ����ͼ���ھ���ABCD�У�AB=8 ![]() ��AD=10����E��CD���е㣬������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غϣ���ͼ2���ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غϣ���ͼ3����B�䵽B�䴦���ۺ�ΪHG������HE�������н�����ȷ�ĸ����ǣ� �� ��ME��HG���ڡ�MEH�ǵȱ������Σ��ۡ�EHG=��AMN����tan��EHG=
��AD=10����E��CD���е㣬������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غϣ���ͼ2���ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غϣ���ͼ3����B�䵽B�䴦���ۺ�ΪHG������HE�������н�����ȷ�ĸ����ǣ� �� ��ME��HG���ڡ�MEH�ǵȱ������Σ��ۡ�EHG=��AMN����tan��EHG= ![]()
A.1��
B.2��
C.3��
D.4��
���𰸡�C
���������⣺��ͼ3�����۵��ɵã���MEN=��A=90�㣬HG��NE�� ��ME��EN��HG��EN��
��EM��GH���ʢ���ȷ��
���NME=��NHG��
���۵��ɵã���NME=��AMN����EHG=��NHG��
���AMN=��EHG���ʢ���ȷ��
��ͼ2����NF��CD��F��
��DM=x����AM=EM=10��x��
�ߵ�E��CD���е㣬AB=CD=8 ![]() ��
��
��DE= ![]() CD=4
CD=4 ![]() ��
��
��Rt��DEM����DM2+DE2=EM2 ��
�ࣨ4 ![]() ��2+x2=��10��x��2 ��
��2+x2=��10��x��2 ��
���x=2.6��
��DM=2.6��AM=EM=7.4��
�ߡ�DEM+��NEF=90�㣬��NEF+��ENF=90�㣬
���DEM=��ENF��
�ߡ�D=��EFN=90�㣬
���DME�ס�FEN��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��EN= ![]() ��
��
��AN= ![]() ��
��
��tan��AMN= ![]() =
= ![]() ��
��
��tan��EHG= ![]() ���ʢ���ȷ��
���ʢ���ȷ��
�֡�tan60��= ![]() ��
�� ![]() ��
��
���AMN��60�㣬����EMH��60�㣬
���MEH���ǵȱ������Σ��ʢڴ���
����ȷ�Ľ�����3����
��ѡ��C��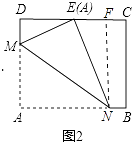
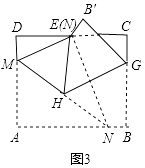
�����㾫����������Ŀ����֪���������þ��ε����ʺͷ��۱任���۵����⣩�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���վ��ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ��۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ�

 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�