题目内容
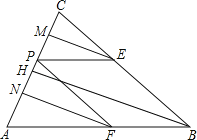
【题目】如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.
【答案】解:(1)证明:∵AB=BC,∴∠A=∠C。
∵PE∥AB,∴∠CPE=∠A。
∴∠CPE=∠C。∴△PCE是等腰三角形。
(2)∵△PCE是等腰三角形,EM⊥CP,∴CM=![]() CP=
CP=![]() ,tanC=tanA=k。
,tanC=tanA=k。
∴EM=CMtanC=![]() k=
k=![]() 。
。
同理:FN=ANtanA=![]() k=4k﹣
k=4k﹣![]() 。
。
由于BH=AHtanA=![]() ×8k=4k,EM+FN=
×8k=4k,EM+FN=![]() +4k﹣
+4k﹣![]() =4k,
=4k,
∴EM+FN=BH。
(3)当k=4时,EM=2x,FN=16﹣2x,BH=16,
∴S△PCE=![]() x2x=x2,S△APF=
x2x=x2,S△APF=![]() (8﹣x)(16﹣2x)=(8﹣x)2,S△ABC=
(8﹣x)(16﹣2x)=(8﹣x)2,S△ABC=![]() ×8×16=64。
×8×16=64。
∴![]() 。
。
∴当k=4时,四边形PEBF的面积S与x的函数关系式为![]() 。
。
∵![]() ,
,
∴当x=4时,S有最大值32。
【解析】(1)根据等边对等角可得∠A=∠C,然后根据两直线平行,同位角相等求出∠CPE=∠A,从而得到∠CPE=∠C,即可得证。
(2)根据等腰三角形三线合一的性质求出CM=![]() CP,然后求出EM,同理求出FN、BH的长,再根据结果整理可得EM+FN=BH。
CP,然后求出EM,同理求出FN、BH的长,再根据结果整理可得EM+FN=BH。
(3)分别求出EM、FN、BH,然后根据S△PCE,S△APF,S△ABC,再根据![]() ,整理即可得到S与x的关系式,然后利用二次函数的最值问题解答。
,整理即可得到S与x的关系式,然后利用二次函数的最值问题解答。

【题目】为了解长城小区“全民健身”活动的开展情况,随机对该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:
锻炼时间(时) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 6 | 13 | 14 | 5 | 2 |
这40名居民一周体育锻炼时间的中位数是 .