Question

【题目】已知：，OB、OM、ON，是 内的射线．

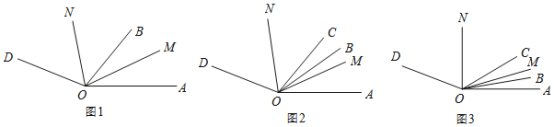
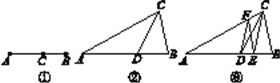
（1）如图 1，若 OM 平分 ， ON平分．当射线OB 绕点O 在 内旋转时，= 度．

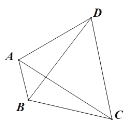
（2）OC也是内的射线，如图2，若 ，OM平分，ON平分，当射线OB绕点O在内旋转时，求的大小．

（3）在（2）的条件下，当射线OB从边OA开始绕O点以每秒的速度逆时针旋转t秒，如图3，若，求t的值．

Answer 1

【答案】（1）80；（2）70°；（3）26

【解析】

（1）根据角平分线的定义进行角的计算即可；
（2）依据OM平分∠AOC，ON平分∠BOD，即可得到∠MOC=∠AOC，∠BON=∠BOD，再根据∠MON=∠MOC+∠BON-∠BOC进行计算即可；
（3）依据∠AOM=（10°+2t+20°），∠DON=（160°-10°-2t），∠AOM：∠DON=2：3，即可得到3（30°+2t）=2（150°-2t），进而得出t的值．

解：（1）∵∠AOD=160°，OM平分∠AOB，ON平分∠BOD，
∴∠MOB=∠AOB，∠BON=∠BOD，
∴∠MON=∠MOB+∠BON=∠AOB+∠BOD=（∠AOB+∠BOD）=∠AOD=80°，

故答案为：80；

（2）∵OM平分∠AOC，ON平分∠BOD，
∴∠MOC=∠AOC，∠BON=∠BOD，
∴∠MON=∠MOC+∠BON-∠BOC
=∠AOC+∠BOD-∠BOC

=（∠AOC+∠BOD）-∠BOC

=×180-20

=70°；
（3）∵∠AOM=（2t+20°），∠DON=（160°-2t），

又∠AOM：∠DON=2：3，

∴3（20°+2t）=2（160°-2t）
解得，t=26．
答：t为26秒．