题目内容
已知Rt△ABC的一边长为10,另两边长恰好是关于x的方程x2-14x+4k-4=0的两个根,则整数k的值为分析:根据勾股定理,以及一元二次方程中根与系数的关系即可解答.不过要分10是斜边和直角边两种情况进行讨论.
解答:解:Rt△ABC的一边长为10,另两边长恰好是关于x的方程x2-14x+4k-4=0的两个根,设为α、β.
(1)边长为10的边是斜边,有α2+β2=(α+β)2-2αβ=142-2(4k-4)=100.求得k=13.
(2)已知边为直角边,
有α2-β2=(α+β)(α-β)=14(α-β)=14
=14
=100
解得k=50-
为分数.故舍去.
(1)边长为10的边是斜边,有α2+β2=(α+β)2-2αβ=142-2(4k-4)=100.求得k=13.
(2)已知边为直角边,
有α2-β2=(α+β)(α-β)=14(α-β)=14
| (α+β)2-4αβ |
| 196-4(4k-4) |
解得k=50-
| 225 |
| 196 |
点评:本题考查一元二次方程根与系数的关系,理解对方程的两边进行讨论是解决本题的关键.

练习册系列答案
相关题目
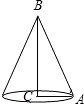 已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )
已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )| A、8π | B、12π | C、15π | D、20π |
已知Rt△ABC的两条直角边AC=3cm,BC=4cm,则以直线AC为轴旋转一周所得到的图形是 ,其侧面积是S= cm2.
| A、圆锥体 | B、圆柱体 | C、长方体 | D、正方体 |
已知Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm,以直线AB为轴旋转一周,得到的几何体的表面积是( )
| A、22.56πcm2 | B、16.8πcm2 | C、9.6πcm2 | D、7.2πcm2 |