题目内容
已知Rt△ABC的周长为12，一直角边为4，则S△ABC=分析：已知一直角边的长及周长，则可以设另一直角边为未知数，根据勾股定理可求得其值，再根据三角形的面积公式即可求得其面积．
解答：解：设另一直角边的长为x．则斜边为12-4-x=8-x
42+x2=（8-x）2
解得x=3
∴S△ABC=
×4×3=6．
42+x2=（8-x）2
解得x=3
∴S△ABC=
| 1 |
| 2 |
点评：此题主要考查学生对勾股定理的理解及运用．
练习册系列答案
相关题目
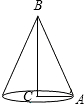已知Rt△ABC的斜边AB=5，一条直角边AC=3，以直线BC为轴旋转一周得到一个圆锥，则这个圆锥的侧面积为（ ）| A、8π | B、12π | C、15π | D、20π |
已知Rt△ABC的两条直角边AC=3cm，BC=4cm，则以直线AC为轴旋转一周所得到的图形是 ，其侧面积是S= cm2．
| A、圆锥体 | B、圆柱体 | C、长方体 | D、正方体 |
已知Rt△ABC的斜边AB=5cm，直角边AC=4cm，BC=3cm，以直线AB为轴旋转一周，得到的几何体的表面积是（ ）
| A、22.56πcm2 | B、16.8πcm2 | C、9.6πcm2 | D、7.2πcm2 |
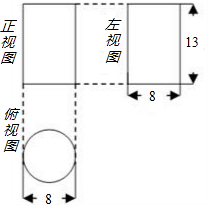（1）已知Rt△ABC的两条直角边AC=3cm，BC=4cm，则以直线BC为轴，旋转一周所得到的几何体的侧面积是