题目内容
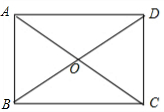 如下图,矩形ABCD的两对角线相交于点O,∠AOD=120°,AC=6cm;
如下图,矩形ABCD的两对角线相交于点O,∠AOD=120°,AC=6cm;(1)判断△AOB的形状;(2)求矩形ABCD各边的长.
分析:(1)由∠AOD=120°可知∠AOB=60°,根据矩形的性质可知AO=BO,所以△AOB是等边三角形.
(2)由(1)可知AB=CD=OB=OC=
AC=3cm,再利用勾股定理可求BC、AD.
(2)由(1)可知AB=CD=OB=OC=
| 1 |
| 2 |
解答:解:(1)∵∠AOD=120°,
∴∠AOB=60°.
∵四边形ABCD是矩形,AO=BO,
∴△AOB是等边三角形.
(2)∵四边形ABCD是矩形,
在Rt△ABC中,AC=6cm,
∴AB=
AC=3cm,BC=3
cm.
∴CD=3cm,AD=3
cm.
∴∠AOB=60°.
∵四边形ABCD是矩形,AO=BO,
∴△AOB是等边三角形.
(2)∵四边形ABCD是矩形,
在Rt△ABC中,AC=6cm,
∴AB=
| 1 |
| 2 |
| 3 |
∴CD=3cm,AD=3
| 3 |
点评:本题主要考查了矩形的性质.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
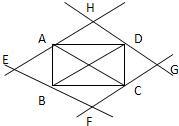 3、如下图过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别交于E、F、G、H四点,则四边形EFGH为( )
3、如下图过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别交于E、F、G、H四点,则四边形EFGH为( )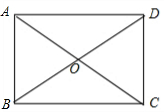 如下图,矩形ABCD的两对角线相交于点O,∠AOD=120°,AC=6cm;
如下图,矩形ABCD的两对角线相交于点O,∠AOD=120°,AC=6cm;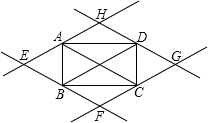
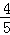 ,求矩形ABCD的面积。
,求矩形ABCD的面积。