题目内容
在下图中,直线l所对应的函数关系式为y=-
x+5,l与y轴交于点C,O为坐标 原点.
原点.
(1)请直接写出线段OC的长;
(2)已知图中A点在x轴的正半轴上,四边形OABC为矩形,边AB与直线l相交于点D,沿直线l把△CBD折叠,点B恰好落在AC上一点E处,并且EA=1.
①试求点D的坐标;
②若⊙P的圆心在线段CD上,且⊙P既与直线AC相切,又与直线DE相交,设圆心P的横坐标为m,试求m的取值范围.
| 1 |
| 5 |
 原点.
原点.(1)请直接写出线段OC的长;
(2)已知图中A点在x轴的正半轴上,四边形OABC为矩形,边AB与直线l相交于点D,沿直线l把△CBD折叠,点B恰好落在AC上一点E处,并且EA=1.
①试求点D的坐标;
②若⊙P的圆心在线段CD上,且⊙P既与直线AC相切,又与直线DE相交,设圆心P的横坐标为m,试求m的取值范围.
(1)OC=5;
(2)①解法一:设D点的横坐标为m,由已知得,
它的纵坐标为:-
m+5
∴BC=OA=m,CA=CE+AE=m+1,
在Rt△OAC中,OA2+OC2=AC2,即m2+52=(m+1)2,
解得m=12.
∴-
m+5=
,即D点的坐标为(12,
);
解法二:设D点的横坐标为m,由已知得,
它的纵坐标为:-
m+5,∴AD=-
m+5,DE=AB-AD=
m,
在Rt△ADE,EA2+ED2=AD2,即12+(
m)2=(-
m+5)2,解得m=12,
∴-
m+5=
,即D点的坐标为(12,
);
解法三:设D点的横坐标为m,由已知得,它的纵坐标为:-
m+5,
在Rt△OAC和Rt△ADE中,∠AOC=∠AED=90°,∠ACO+∠OAC=90°,∠OAC+∠EAD=90°,
∴∠ACO=∠EAD,
∴Rt△OAC∽Rt△ADE,
∴
=
,即:
=
,解得m=12,
∴-
m+5=
,即D点的坐标为(12,
);
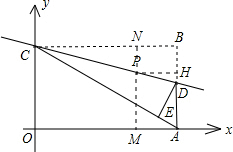
②由于△BCD和△CDE关于直线L对称,
所以⊙P与直线AC相切,与DE相交相当于与直线BC相切,与BD相交,
过点P作PM⊥OA,交OA于M,交BC于N;作PH⊥AB,交AB于H,
由题意知:只要PN>PH即可,
PN=MN-PM=
m,PH=12-m,即:
m>12-m,解得m>10,
又P在线段CD上,所以m≤12,
即m的取值范围是10<m≤12.
(2)①解法一:设D点的横坐标为m,由已知得,
它的纵坐标为:-
| 1 |
| 5 |
∴BC=OA=m,CA=CE+AE=m+1,
在Rt△OAC中,OA2+OC2=AC2,即m2+52=(m+1)2,
解得m=12.
∴-
| 1 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
解法二:设D点的横坐标为m,由已知得,
它的纵坐标为:-
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
在Rt△ADE,EA2+ED2=AD2,即12+(
| 1 |
| 5 |
| 1 |
| 5 |
∴-
| 1 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
解法三:设D点的横坐标为m,由已知得,它的纵坐标为:-
| 1 |
| 5 |
在Rt△OAC和Rt△ADE中,∠AOC=∠AED=90°,∠ACO+∠OAC=90°,∠OAC+∠EAD=90°,
∴∠ACO=∠EAD,
∴Rt△OAC∽Rt△ADE,
∴
| AC |
| AD |
| OC |
| AE |
| m+1 | ||
-
|
| 5 |
| 1 |
∴-
| 1 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |

②由于△BCD和△CDE关于直线L对称,
所以⊙P与直线AC相切,与DE相交相当于与直线BC相切,与BD相交,
过点P作PM⊥OA,交OA于M,交BC于N;作PH⊥AB,交AB于H,
由题意知:只要PN>PH即可,
PN=MN-PM=
| 1 |
| 5 |
| 1 |
| 5 |
又P在线段CD上,所以m≤12,
即m的取值范围是10<m≤12.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目







