题目内容
【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点M在BC边上，且∠MDF=∠ADF．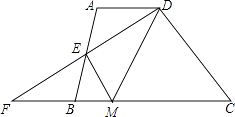 
（1）求证：△ADE≌△BFE．
（2）如果FM=CM，求证：EM垂直平分DF．
【答案】
（1）证明：∵AD∥BC，
∴∠A=∠EBF，∠ADE=∠F．
∵E是AB的中点，
∴AE=BE．
在△ADE与△BFE中，
，
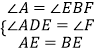∴△ADE≌△BFE（AAS）
（2）证明：∵AD∥BC，
∴∠ADE=∠F．
∵∠MDF=∠ADF，
∴∠MDF=∠F．
∴FM=DM．
∵△ADE≌△BFE，
∴EF=DE．
∴点E为边DF的中点．
∴ME⊥DF．
即EM垂直平分DF
【解析】（1）根据AD∥BC，可得∠A=∠EBF，∠ADE=∠F，由E是AB的中点，可得AB=BE，从而可以证明△ADE≌△BFE；（2）由△ADE≌△BFE，可得DE与EF相等，点E为DF的中点，再根据∠MDF=∠ADF，AD∥BC，FM=CM，可以得到MF=MD，然后根据等腰三角形三线合一，可以证明结论成立．
【考点精析】利用线段垂直平分线的性质对题目进行判断即可得到答案，需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】（10分）下面的图形是由边长为l的正方形按照某种规律排列而组成的．
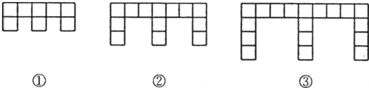
（1）观察图形，填写下表：
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
（2）推测第n个图形中，正方形的个数为 ，周长为 （都用含n的代数式表示）．
（3）这些图形中，任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= ．
