Question

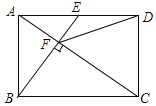
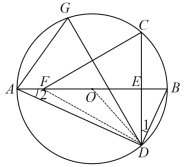
【题目】如图，C，D为⊙O上两点，且在直径AB两侧，连结CD交AB于点E，G是上一点，∠ADC＝∠G．

（1）求证：∠1＝∠2；

（2）点C关于DG的对称点为F，连结CF，当点F落在直径AB上时，CF＝10，tan∠1＝，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据∠ADC＝∠G得，进而可得，由此可得∠1＝∠2；

（2）连接OD、FD，先证FC＝FD，FD＝CD，进而可得FC＝FD＝CD＝10，DE＝CD＝5，再根据tan∠1＝可得BE＝2，设OB＝OD＝x，则OE＝5－x，根据勾股定理即可求得⊙O的半径．

（1）证明：∵∠ADC＝∠G，

∴，

∵AB为⊙O的直径，

∴

∴，

∴，

∴∠1＝∠2；

（2）解：连接OD、FD，

∵，，

∴点C、D关于直径AB对称，

∴AB垂直平分CD，

∴FC＝FD，CE＝DE＝CD，∠DEB＝90°，

∵点C关于DG的对称点为F，

∴DG垂直平分FC，

∴FD＝CD，

又∵CF＝10，

∴FC＝FD＝CD＝10，

∴DE＝CD＝5，

∵在Rt△DEB中，tan∠1＝

∴，

∴，

∴BE＝2，

设OB＝OD＝x，则OE＝5－x，

∵在Rt△DOE中，，

∴，

解得：

∴⊙O的半径为．