题目内容
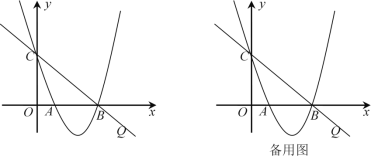
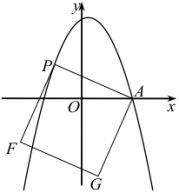
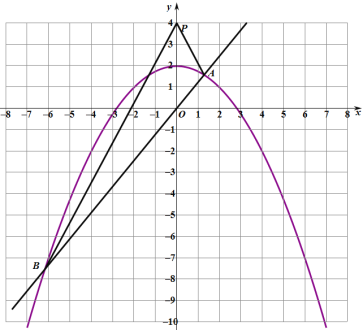
【题目】在平面直角坐标系xoy中,直线![]() (k为常数)与抛物线
(k为常数)与抛物线![]() 交于A,B两点,且A点在
交于A,B两点,且A点在![]() 轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当
轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当![]() 时,
时,![]() =_______
=_______
【答案】![]() 16
16
【解析】
(1)设A(m,km),B(n,kn),联立解析式,利用根与系数的关系建立![]() 之间的关系,列出面积函数关系式,利用二次函数的性质求解最小值即可;
之间的关系,列出面积函数关系式,利用二次函数的性质求解最小值即可;
(2)先证明![]() 平分
平分![]() 得到
得到![]() ,把
,把![]() 转化为
转化为![]() ,利用两点间的距离公式再次转化,从而可得答案.
,利用两点间的距离公式再次转化,从而可得答案.
解:(1)如图,设A(m,km),B(n,kn),其中m![]() 0,n
0,n![]() 0.
0.
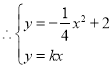
得: ![]() 即
即![]() ,
,
∴![]()
![]()
![]()
∴当k=0时,△PAB面积有最小值,最小值为![]()
故答案为![]() .
.
(2)设设A(m,km),B(n,kn),其中m![]() 0,n
0,n![]() 0.
0.
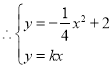
得: ![]() 即
即![]() ,
,
∴![]()
设直线PA的解析式为y=ax+b,将P(0,4),A(m,km)代入得:
![]() ,解得:
,解得: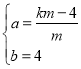 ,
,
∴![]()
令y=0,得![]()
∴直线PA与x轴的交点坐标为![]() .
.
同理可得,直线PB的解析式为![]()
直线PB与x轴交点坐标为![]() .
.
∵ 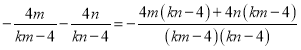

∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
![]() 平分
平分![]() ,
,
![]()
![]() 到
到![]() 的距离相等,
的距离相等,
![]()
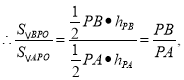
而 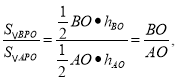
∴![]() ,
,
过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,
则![]()
![]()
∴![]()
∴![]()
![]()
![]()
![]()
∵![]() ∴
∴![]()
∴![]()
∴![]()

故答案为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目