题目内容
【题目】如图,直线l1:y1=![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.

【答案】(1)D点坐标为(4,3)(2)15;(3)x<4
【解析】试题分析:(1)先得到两函数的解析式,组成方程组解求出D的坐标;(2)由y2=![]()
x+1可知,C点坐标为(0,1),分别求出△ABC和△ACD的面积,相加即可.(3)由图可直接得出y1>y2时自变量x的取值范围.
试题解析:(1)将A(0,6)代入y1=![]() x+m得,m=6;将B(-2,0)代入y2=kx+1得,k=
x+m得,m=6;将B(-2,0)代入y2=kx+1得,k=![]()
组成方程组得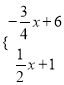 解得
解得![]() 故D点坐标为(4,3);
故D点坐标为(4,3);
(2)由y2=![]() x+1可知,C点坐标为(0,1),S△ABD=S△ABC+S△ACD=
x+1可知,C点坐标为(0,1),S△ABD=S△ABC+S△ACD=![]() ×5×2+
×5×2+![]() ×5×4=15;
×5×4=15;
(3)由图可知,在D点左侧时,y1>y2,即x<4时,出y1>y2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某手机销售商分别以每部进价分别为800元、670元的A、B两种型号的手机,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 6台 | 7650元 |
第二周 | 4台 | 10台 | 11800元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的手机的销售单价;
(2)若手机销售商准备再采购这两种型号的手机共30台,且利润不低于4000元,求A种型号的手机至少要采购多少台?