Question

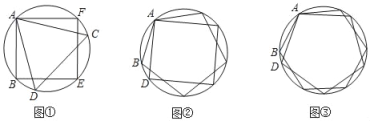
【题目】如图①，正三角形和正方形内接于同一个圆；如图②，正方形和正五边形内接于同一个圆；如图③，正五边形和正六边形内接于同一个圆；…；则对于图①来说，BD可以看作是正_____边形的边长；若正n边形和正（n+1）边形内接于同一个圆，连接与公共顶点相邻同侧两个不同正多边形的顶点可以看做是_____边形的边长．

Answer 1

【答案】十二； 正n（n+1）

【解析】

如图①，连接OA、OB、OD，先计算出∠AOD＝120°，∠AOB＝90°，则∠BOD＝30°，然后计算可判断BD是正十二边形的边长；对于正n边形和正（n+1）边形内接于同一个圆，同样计算出∠BOD＝∠AOD﹣∠AOB＝，利用＝n（n+1）可判断BD可以看作是正 n（n+1）边形的边长．

如图，连接OA、OB、OD，

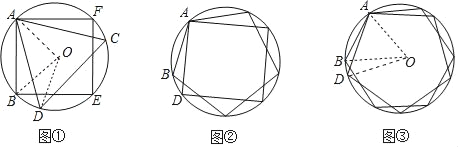
∵正三角形ADC和正方形ABCD接于同一个⊙O，

∴∠AOD＝＝120°，∠AOB＝＝90°，

∴∠BOD＝∠AOD﹣∠AOB＝30°，

∵＝12，

∴BD可以看作是正 十二边形的边长；

若正n边形和正（n+1）边形内接于同一个圆，

同理可得∠AOD＝，∠AOB＝，

∴∠BOD＝∠AOD﹣∠AOB＝﹣＝，

∵＝n（n+1），

∴BD可以看作是正 n（n+1）边形的边长．

故答案为十二；正n（n+1）．