题目内容
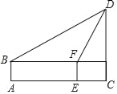
【题目】如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F.
(1)求证:DE=DF;
(2)当BC=3,sinA=![]() 时,求AE的长.
时,求AE的长.
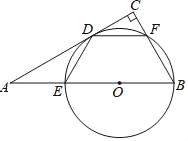
【答案】(1)见解析;(2)AE=![]() .
.
【解析】
(1)连接OD,OF,由切线的性质可得∠ADO=90°,从而得到OD∥BC,从而得到∠AOD=∠ABC,∠DOF=∠OFB,并由半径相等,再进行角的代换从而得到∠AOD=∠DOF,即可求解.
(2) Rt△ABC中,有正弦的定义求出AB,再由Rt△AOD中,设圆的半径为r,通过正弦建立比例式方程从而进行求解.
解:(1)如图所示,连接OD,OF,
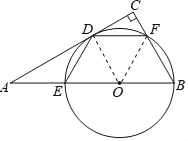
∵⊙O与AC相切于点D,
∴∠ADO=90°,
∵∠ACB=90°,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOF=∠OFB,
∵OB=OF,
∴∠ABC=∠OFB,
∴∠AOD=∠DOF,
∴DE=DF;
(2)在Rt△ABC中,∵BC=3,sinA=![]() =
=![]() ,
,
∴AB=5,
设⊙O的半径为r,则OB=OD=OE=r,
则AO=AB﹣OB=5﹣r,AE=5﹣2r,
在Rt△AOD中,∵sinA=![]() =
=![]() ,
,
∴![]() =
=![]() ,解得r=
,解得r=![]() ,
,
则AE=5﹣2r=![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目