��Ŀ����
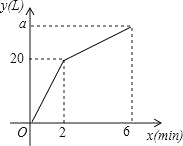
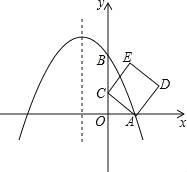
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+2��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B����Գ�����x=-1����C��y����һ�㣬��������Ϊm������AC�����߶�AC�Ƶ�A˳ʱ����ת90��õ��߶�AD����AC��ADΪ����������ACED��
��1���ú�m�Ĵ���ʽ��ʾ��D�ĺ�����Ϊ ��
��2���������������Ӧ�ĺ�������ʽ��
��3������E����������y=ax2+bx+2��ʱ�����ʱm��ֵ��
��4������������x����һ����Ϊ��F������BF��ֱ��д��������ACED��һ����BFƽ��ʱ��m��ֵ��
���𰸡���1��m+1����2��y=-![]() x2-
x2-![]() x+2����3��
x+2����3��![]() ��
��![]() ����4��
����4��![]() ��-
��-![]() ��
��
��������
�����������1����DH��x����H����ͼ1�������õȽǵ������ȵõ���ACO=��DAH����ɸ��ݡ�AAS��֤����ACO�ա�DAH������AH=OC=m���õ�D�ĺ�����Ϊm+1��
��2�����öԳ��᷽�̺Ͷ��κ���ͼ���ϵ�����������з����� ���ⷽ�������a��b���ɵõ������ߵĽ���ʽ��
���ⷽ�������a��b���ɵõ������ߵĽ���ʽ��
��3����EG��y����G����ͼ1��ͨ���루1������һ��֤����ACO�ա�CEG�õ�GE=OC=m��CG=OA=1����E������Ϊ��m��m+1����Ȼ���E��������루2���н���ʽ�õ�����m�ķ��̣��ٽⷽ�̼��ɵõ�m��ֵ��
��4����ͨ���ⷽ��-![]() x2-
x2-![]() x+2=0��F��-3��0�������㵱x=0ʱ�ĺ���ֵ�õ�B��0��2�������ۣ�����C��y����������ϣ���m��0ʱ����ͼ1��֤����ADH�ס�FBO���������Ʊȿɵõ�m��ֵ������C��y��ĸ������ϣ���m��0ʱ����ͼ2��֤����AOC�ס�FOB���������Ʊȿɼ����m��
x+2=0��F��-3��0�������㵱x=0ʱ�ĺ���ֵ�õ�B��0��2�������ۣ�����C��y����������ϣ���m��0ʱ����ͼ1��֤����ADH�ס�FBO���������Ʊȿɵõ�m��ֵ������C��y��ĸ������ϣ���m��0ʱ����ͼ2��֤����AOC�ס�FOB���������Ʊȿɼ����m��
�����������1����DH��x����H����ͼ1��

���ı���ADECΪ�����Σ�
��AC=AD����CAD=90�㣬
�ߡ�CAO+��ACO=90�㣬��CAO+��DAH=90�㣬
���ACO=��DAH��
�ڡ�ACO�͡�DAH�У�
 ��
��
���ACO�ա�DAH��
��AH=OC=m��
��OH=OA+AH=m+1��
���D�ĺ�����Ϊm+1��
��2����������� �����
����� ��
��
�������ߵĽ���ʽΪy=-![]() x2-
x2-![]() x+2��
x+2��
��3����EG��y����G����ͼ1��
�루1������һ����֤���á�ACO�ա�CEG����GE=OC=m��CG=OA=1��
��E��������m��m+1����
��E��m��m+1������y=-![]() x2-
x2-![]() x+2��-
x+2��-![]() m2-
m2-![]() m+2=m+1��
m+2=m+1��
������2m2+7m-3=0�����m1=![]() ��m2=
��m2=![]() ��
��
��m��ֵΪ![]() ��
��![]() ��
��
��4����y=0ʱ��-![]() x2-
x2-![]() x+2=0�����x1=-3��x2=1����F��-3��0����
x+2=0�����x1=-3��x2=1����F��-3��0����
��x=0ʱ��y=-![]() x2-
x2-![]() x+2=2����B��0��2����
x+2=2����B��0��2����
����C��y����������ϣ���m��0ʱ����ͼ1��
��AD��BF��
���DAH=��BFO��
���ADH�ס�FBO��
��AH��OF=DH��OB����m��3=1��2�����m=![]() ��
��
����C��y��ĸ������ϣ���m��0ʱ����ͼ2��

��AC��BF��
���ACO=��OBF��
���AOC�ס�FOB��
��AO��OF=OC��OB��1����1��3=-m��2�����m=-![]() ��
��
��m��ֵΪ![]() ��-
��-![]() ��
��