题目内容
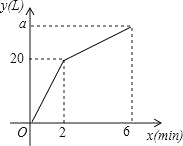
【题目】一个容器装有一个注水管和两个排水管,每个排水管每分钟排水7.5L,从某一时刻开始2min内只注水不排水,2min后开启一个排水管,容器内的水量y(L)与注水时间x(min)之间的函数关系如图所示.
(1)求a的值.
(2)当2≤x≤6时,求y与x的函数关系式.
(3)若在6min之后,两个出水管均开启,注水管关闭,还需多长时间可排尽容器中的水?
【答案】(1)30;(2)y=![]() x+15(2≤x≤6);(3)2小时.
x+15(2≤x≤6);(3)2小时.
【解析】
试题分析: (1)每分钟的进水量根据前2分钟的图象求出,根据后4分钟的水量变化即可求得a的值.
(2)设当2≤x≤6时,y与x的函数关系式为y=kx+b.图象过(2,20)、(6,30),用待定系数法求对应的函数关系式;
(3)根据每个出水管每分钟出水量,即可求得排完容器的水所有的时间.
试题解析:(1)根据图象,每分钟进水20÷2=10L,
在随后的4min内容器内的水量y=4(10﹣7.5)=10(L),
∴a=20+10=30;
(2)设当2≤x≤6时,y与x的函数关系式为y=kx+b.
∵图象过(2,20)、(6,30),
∴![]() ,
,
解得: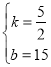 ,
,
∴当2≤x≤6时,y与x的函数关系式为y=![]() x+15(2≤x≤6);
x+15(2≤x≤6);
(3)30÷(2×7.5)=2.
答:还需2小时可排尽容器中的水.

练习册系列答案
相关题目