题目内容
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
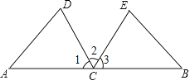
(1)求证:△ACD≌△BCE;
(2)若∠D=75°,求∠B的度数.
【答案】(1)详见解析;(2)45°.
【解析】
(1)先利用角平分线性质、以及等量代换,可证出∠1=∠3,结合CD=CE,C是AB中点,即AC=BC,利用SAS可证全等;
(2)利用角平分线性质,可知∠1=∠2,∠2=∠3,从而求出∠1=∠2=∠3,再利用全等三角形的性质可得出∠E=∠D,在△BCE中,利用三角形内角和是180°,可求出∠B.
(1)证明:∵点C是线段AB的中点,
∴AC=BC,
又∵CD平分∠ACE,CE平分∠BCD,
∴∠1=∠2,∠2=∠3,
∴∠1=∠3,
∵在△ACD和△BCE中,
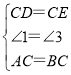 ,
,
∴△ACD≌△BCE(SAS).
(2)∵∠1+∠2+∠3=180°,
∴∠1=∠2=∠3=60°,
∵△ACD≌△BCE,
∴∠E=∠D=75°,
∴∠B=180°-∠E-∠3=180°-75°-60°=45°.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】学校让综合实践活动课外学习小组参与学校校办工厂的足球生产活动,在工人师傅的指导和帮助下,综合实践活动课外学习小组一周计划生产700个足球,平均每天生产100个,由于各种原因实际每天生产产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前四天共生产 个;
(2)产量最多的一天比产量最少的一天多生产 个;
(3)该校办工厂实行每周计件奖励制,生产一个足球奖励给综合实践活动课外学习小组![]() 元.超额完成任务超额部分每个再奖
元.超额完成任务超额部分每个再奖![]() 元,那么该校的综合实践活动课外学习小组这一周得到的奖励总额是多少元?
元,那么该校的综合实践活动课外学习小组这一周得到的奖励总额是多少元?