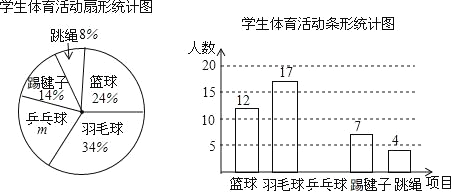
题目内容
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.

【答案】1或![]() 或12.
或12.
【解析】
根据题意进行分类讨论,根据全等三角形的性质得出CP=CQ,代入得出关于t的方程,求出即可.
①如图1,P在AC上,Q在BC上,
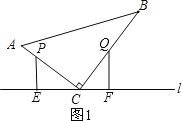
∵PE⊥l,QF⊥l,
∴∠PEC=∠QFC=90°,
∵∠ACB=90°,
∴∠EPC+∠PCE=90°,∠PCE+∠QCF=90°,
∴∠EPC=∠QCF,
则△PCE≌△CQF,
∴PC=CQ,
即6-t=8-3t,
t=1;
②如图2,P在BC上,Q在AC上,
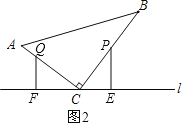
∵由①知:PC=CQ,
∴t-6=3t-8,
t=1;
t-6<0,即此种情况不符合题意;
③当P、Q都在AC上时,如图3,
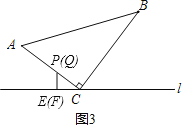
CP=6-t=3t-8,
t=![]() ;
;
④当Q到A点停止,P在BC上时,AC=PC,t-6=6时,解得t=12.
∵P的速度是每秒1cm,Q的速度是每秒3cm,
P和Q都在BC上的情况不存在.
故答案为:1或![]() 或12.
或12.

练习册系列答案
相关题目