题目内容
如图,已知⊙B的半径r=1,PA、PO是⊙B的切线,A、O是切点.过点A作弦AC∥PO,连接CO、AO(如图1).(1)问△PAO与△OAC有什么关系?证明你的结论;
(2)把整个图形放在直角坐标系中(如图2),使OP与x轴重合,B点在y轴上.
设P(t,0),P点在x轴的正半轴上运动时,四边形PACO的形状随之变化,当这图形满足什么条件时,四边形PACO是菱形?说明理由.
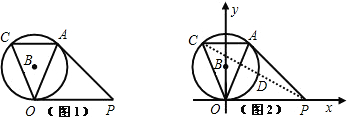
分析:(1)两三角形相似,根据平行线可得一组对应角相等,根据弦切角可得另一组对应角相等;
(2)如果PACO是菱形,那么PA=PO=OC=OA=AC,△OAC就是等边三角形,那么可过B作等边三角形边上的高,通过构建的直角三角形来求t的值.
(2)如果PACO是菱形,那么PA=PO=OC=OA=AC,△OAC就是等边三角形,那么可过B作等边三角形边上的高,通过构建的直角三角形来求t的值.
解答: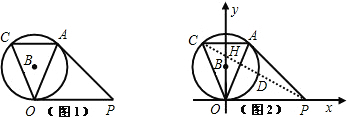 解:(1)结论:两三角形相似.
解:(1)结论:两三角形相似.
证明:∵PA是圆的切线,
∴∠PAO=∠C
∵AC∥PO
∴∠CAO=∠POA
∴△PAO∽△OCA;
(2)当四边形PACO是菱形时,PA=PO=OC=AC=t
∵PA=OP,△PAO∽△OCA
∴OC=OA
∴△OCA是等边三角形
过B作BH⊥AC于H,连接BC,
直角△BCH中,∠CBH=60°,BC=1,CH=
CH=BC•sin60°=
=
,
t=
因此当P点坐标是(
,0)时,四边形PACO是菱形.
 解:(1)结论:两三角形相似.
解:(1)结论:两三角形相似.证明:∵PA是圆的切线,
∴∠PAO=∠C
∵AC∥PO
∴∠CAO=∠POA
∴△PAO∽△OCA;
(2)当四边形PACO是菱形时,PA=PO=OC=AC=t
∵PA=OP,△PAO∽△OCA
∴OC=OA
∴△OCA是等边三角形
过B作BH⊥AC于H,连接BC,
直角△BCH中,∠CBH=60°,BC=1,CH=
| t |
| 2 |
CH=BC•sin60°=
| ||
| 2 |
| 1 |
| 2 |
t=
| 3 |
因此当P点坐标是(
| 3 |
点评:本题主要考查了切线的性质,菱形的判定以及相似三角形的判定和性质等知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
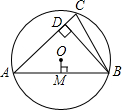 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
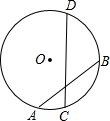 如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
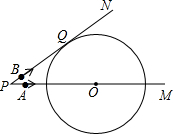 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.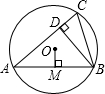 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD= (2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.