题目内容
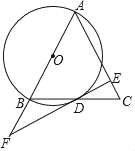
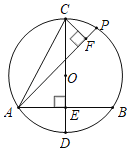
【题目】如图,在半径为2的⊙O中,弦AB⊥直径CD,垂足为E,∠ACD=30°,点P为⊙O上一动点,CF⊥AP于点F.
①弦AB的长度为_____;
②点P在⊙O上运动的过程中,线段OF长度的最小值为_____.
【答案】2![]() .
. ![]() -1
-1
【解析】
①在Rt△AOE中,解直角三角形求出AE即可解决问题.
②取AC的中点H,连接OH,OF,HF,求出OH,FH,根据OF≥FH-OH,即![]() ,由此即可解决问题.
,由此即可解决问题.
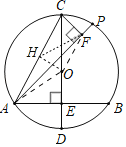
解:①如图,连接OA.
∵OA=OC=2,
∴∠OCA=∠OAC=30°,
∴∠AOE=∠OAC+∠ACO=60°,
∴AE=OAsin60°=![]() ,
,
∵OE⊥AB,
∴AE=EB=![]() ,
,
∴AB=2AE=2![]() ,
,
故答案为2![]() .
.
②取AC的中点H,连接OH,OF,HF,
∵OA=OC,AH=HC,
∴OH⊥AC,
∴∠AHO=90°,
∵∠COH=30°,
∴OH=![]() OC=1,HC=
OC=1,HC=![]() ,AC=2
,AC=2![]() ,
,
∵CF⊥AP,
∴∠AFC=90°,
∴HF=![]() AC=
AC=![]() ,
,
∴OF≥FH﹣OH,即OF≤![]() ﹣1,
﹣1,
∴OF的最小值为![]() ﹣1.
﹣1.
故答案为![]() ﹣1.
﹣1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色.
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小 明每次換出一个小球记录下慎色并放回,实验数据如下表:
实验次数 | 100 | 200 | 300 | 400 | 500 | 1000 |
摸出红球 | 78 | 147 | 228 | 304 | 373 | 752 |
请你帮小明算出老师放入了多少个红色小球.