题目内容
锐角△ABC中,BC=6, 两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,

 两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,

公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.为正方形时可求出面积的值,为矩形时需求面积表达式再求最大值.
解:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.
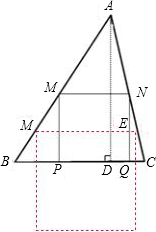
(1)求公共部分是正方形时的面积,
作AD⊥BC于D点,交MN于E点,
∵BC=6,S△ABC=12,
∴AD=4,
∵MN∥BC,
∴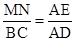 即
即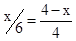 ,
,
解得x=2.4,
此时面积y=2.42=5.76.
(2)当公共部分是矩形时如图所示:
设DE=a,根据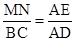 得
得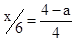 ,
,
所以a=4-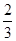 x,公共部分的面积y=x(4-
x,公共部分的面积y=x(4-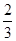 x)=-
x)=-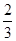 x2+4x,
x2+4x,
∵-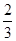 <0,
<0,
∴y有最大值,
当x=-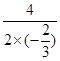 =3时,y最大值=
=3时,y最大值=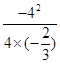 =6.
=6.
综上所述,当x=3时,公共部分的面积y最大,最大值为6.
解:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.

(1)求公共部分是正方形时的面积,
作AD⊥BC于D点,交MN于E点,
∵BC=6,S△ABC=12,
∴AD=4,
∵MN∥BC,
∴
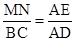 即
即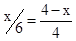 ,
,解得x=2.4,
此时面积y=2.42=5.76.
(2)当公共部分是矩形时如图所示:
设DE=a,根据
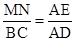 得
得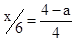 ,
,所以a=4-
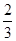 x,公共部分的面积y=x(4-
x,公共部分的面积y=x(4-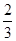 x)=-
x)=-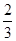 x2+4x,
x2+4x,∵-
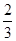 <0,
<0,∴y有最大值,
当x=-
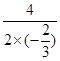 =3时,y最大值=
=3时,y最大值=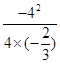 =6.
=6.综上所述,当x=3时,公共部分的面积y最大,最大值为6.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目


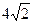 cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。