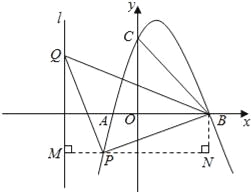
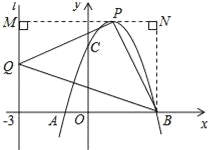
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßL£ŗy=ax2+bx+cÓėxÖį½»ÓŚA”¢B£Ø3£¬0£©Į½µć£ØAŌŚBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£Ø0£¬3£©£¬ŅŃÖŖ¶Ō³ĘÖįx=1£®
£Ø1£©ĒóÅ×ĪļĻßLµÄ½āĪöŹ½£»
£Ø2£©½«Å×ĪļĻßLĻņĻĀĘ½ŅĘhøöµ„Ī»³¤¶Č£¬Ź¹Ę½ŅĘŗóĖłµĆÅ×ĪļĻߵĶ„µćĀäŌŚ”÷OBCÄŚ£Ø°üĄØ”÷OBCµÄ±ß½ē£©£¬ĒóhµÄȔֵ·¶Ī§£»
£Ø3£©ÉčµćPŹĒÅ×ĪļĻßLÉĻČĪŅ»µć£¬µćQŌŚÖ±Ļßl£ŗx=©3ÉĻ£¬”÷PBQÄÜ·ń³ÉĪŖŅŌµćPĪŖÖ±½Ē¶„µćµÄµČŃüÖ±½ĒČż½ĒŠĪ£æČōÄÜ£¬Ēó³ö·ūŗĻĢõ¼žµÄµćPµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ(1)y=©x2+2x+3£»(2)2”Üh”Ü4£»(3)£Ø1£¬4£©£¬£Ø0£¬3£©£¬£Ø![]() £¬
£¬![]() £©ŗĶ£Ø
£©ŗĶ£Ø![]() £¬
£¬![]() £©£®
£©£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ(1)”¢ĄūÓĆ“ż¶ØĻµŹż·ØĒó³öÅ×ĪļĻߵĽāĪöŹ½¼“æÉ£»(2)”¢ĻČĒó³öÖ±ĻßBC½āĪöŹ½ĪŖy=©x+3£¬ŌŁĒó³öÅ×ĪļĻ߶„µć×ų±ź£¬µĆ³öµ±x=1Ź±£¬y=2£»½įŗĻÅ×ĪļĻ߶„µć×ų¼“æÉµĆ³ö½į¹ū£»(3)”¢ÉčP£Øm£¬©m2+2m+3£©£¬Q£Ø©3£¬n£©£¬Óɹ“¹É¶ØĄķµĆ³öPB2=£Øm©3£©2+£Ø©m2+2m+3£©2£¬PQ2=£Øm+3£©2+£Ø©m2+2m+3©n£©2£¬BQ2=n2+36£¬¹żPµć×÷PM“¹Ö±ÓŚyÖį£¬½»yÖįÓėMµć£¬¹żBµć×÷BN“¹Ö±ÓŚMPµÄŃÓ³¤ĻßÓŚNµć£¬ÓÉAASÖ¤Ć÷”÷PQM”Õ”÷BPN£¬µĆ³öMQ=NP£¬PM=BN£¬ŌņMQ=©m2+2m+3©n£¬PN=3©m£¬µĆ³ö·½³Ģ©m2+2m+3©n=3©m£¬½ā·½³Ģ¼“æÉ£®
ŹŌĢā½āĪö£ŗ(1)”¢”ßÅ×ĪļĻߵĶŌ³ĘÖįx=1£¬B£Ø3£¬0£©£¬ ”ąA£Ø©1£¬0£© ”ßÅ×ĪļĻßy=ax2+bx+c¹żµćC£Ø0£¬3£©
”ąµ±x=0Ź±£¬c=3£® ÓÖ”ßÅ×ĪļĻßy=ax2+bx+c¹żµćA£Ø©1£¬0£©£¬B£Ø3£¬0£©
”ą![]() £¬ ”ą
£¬ ”ą![]() ”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗy=©x2+2x+3£»
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗy=©x2+2x+3£»
(2)”¢”ßC£Ø0£¬3£©£¬B£Ø3£¬0£©£¬ ”ąÖ±ĻßBC½āĪöŹ½ĪŖy=©x+3£¬ ”ßy=©x2+2x+3=©£Øx©1£©2+4£¬
”ą¶„µć×ų±źĪŖ£Ø1£¬4£© ”߶ŌÓŚÖ±ĻßBC£ŗy=©x+1£¬µ±x=1Ź±£¬y=2£»½«Å×ĪļĻßLĻņĻĀĘ½ŅĘhøöµ„Ī»³¤¶Č£¬[Ō“:”ąµ±h=2Ź±£¬Å×ĪļĻ߶„µćĀäŌŚBCÉĻ£» µ±h=4Ź±£¬Å×ĪļĻ߶„µćĀäŌŚOBÉĻ£¬
”ą½«Å×ĪļĻßLĻņĻĀĘ½ŅĘhøöµ„Ī»³¤¶Č£¬Ź¹Ę½ŅĘŗóĖłµĆÅ×ĪļĻߵĶ„µćĀäŌŚ”÷OBCÄŚ£Ø°üĄØ”÷OBCµÄ±ß½ē£©£¬
Ōņ2”Üh”Ü4£»
(3)”¢ÉčP£Øm£¬©m2+2m+3£©£¬Q£Ø©3£¬n£©£¬
¢Łµ±PµćŌŚxÖįÉĻ·½Ź±£¬¹żPµć×÷PM“¹Ö±ÓŚyÖį£¬½»yÖįÓėMµć£¬¹żBµć×÷BN“¹Ö±ÓŚMPµÄŃÓ³¤ĻßÓŚNµć£¬ČēĶ¼ĖłŹ¾£ŗ ”ßB£Ø3£¬0£©£¬ ”ß”÷PBQŹĒŅŌµćPĪŖÖ±½Ē¶„µćµÄµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻBPQ=90”ć£¬BP=PQ£¬ Ōņ”ĻPMQ=”ĻBNP=90”ć£¬”ĻMPQ=”ĻNBP£¬ ŌŚ”÷PQMŗĶ”÷BPNÖŠ£¬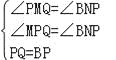 £¬
£¬
”ą”÷PQM”Õ”÷BPN£ØAAS£©£¬ ”ąPM=BN£¬ ”ßPM=BN=©m2+2m+3£¬øł¾ŻBµć×ų±źæɵĆPN=3©m£¬ĒŅPM+PN=6£¬
”ą©m2+2m+3+3©m=6£¬ ½āµĆ£ŗm=1»ņm=0£¬ ”ąP£Ø1£¬4£©»ņP£Ø0£¬3£©£®
¢Śµ±PµćŌŚxÖįĻĀ·½Ź±£¬¹żPµć×÷PM“¹Ö±ÓŚlÓŚMµć£¬¹żBµć×÷BN“¹Ö±ÓŚMPµÄŃÓ³¤ĻßÓėNµć£¬
Ķ¬ĄķæɵƔ÷PQM”Õ”÷BPN£¬ ”ąPM=BN£¬ ”ąPM=6©£Ø3©m£©=3+m£¬BN=m2©2m©3£¬ Ōņ3+m=m2©2m©3£¬
½āµĆm=![]() »ņ
»ņ![]() £® ”ąP£Ø
£® ”ąP£Ø![]() £¬
£¬![]() £©»ņ£Ø
£©»ņ£Ø![]() £¬
£¬![]() £©£®
£©£®
×ŪÉĻæÉµĆ£¬·ūŗĻĢõ¼žµÄµćPµÄ×ų±źŹĒ£Ø1£¬4£©£¬£Ø0£¬3£©£¬£Ø![]() £¬
£¬![]() £©ŗĶ£Ø
£©ŗĶ£Ø![]() £¬
£¬![]() £©£®
£©£®