Question

【题目】如图，直线DE经过点A，DE∥BC，∠B=45°，∠C=50°，

（1）求∠DAB的度数，并写出理由.

（2）求∠EAC的度数.

（3）计算∠BAC的度数.

（4）根据以上条件及结论，你还能得出其他结论吗？试写出一个.

Answer 1

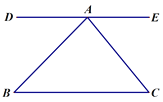
【答案】（1）∠DAB的度数为45°，根据两直线平行，内错角相等得出.（2）∠EAC的度数是50°.（3）∠BAC=180°-∠DAB-∠EAC=180°-45°-50°=95°.（4）三角形ABC的内角和是180°

【解析】（1）由平行线的性质可得到∠DAB=∠B；（2）由平行线的性质可得到∠EAC=∠C；（3）由平角的定义可求得∠BAC，（4）结合（1）（2）（3）可得出结论．

解：（1）∵DE∥BC，
∴∠DAB=∠B=45°；
（2）∵DE∥BC，
∴∠EAC=∠C=50°，
（3）∵直线DE过点A，
∴∠DAE=180°，
∴∠DAB+∠EAC+∠BAC=180°，
∴∠BAC=180°-45°-50°=85°；
（4）∵DE∥BC，
∴∠B=∠DAB，∠C=∠EAC，
∵∠DAB+∠EAC+∠BAC=180°，
∴∠B+∠C+∠BAC=180°，
即三角形内角和为180°．

“点睛”本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，④a∥b，b∥c，a∥c．