题目内容
【题目】如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
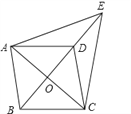
(1)四边形ABCD是菱形吗?请说明理由;
(2)若∠AED=2∠EAD,试说明四边形ABCD是正方形.
【答案】(1)四边形ABCD是菱形,理由见解析;(2)理由见解析.
【解析】分析:(1)根据对角线互相垂直的平行四边形是菱形.∵△ACE是等边三角形,∴EO⊥AC(三线合一),即AC⊥BD.∴四边形ABCD是菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠DAO=∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠DAB=2∠ADO=90°,∴四边形ABCD是正方形.
解:(1)四边形ABCD是菱形,理由如下:
∵四边形ABCD是平行四边形 ∴OA=OC,即O是AC的中点.
∵△ACE是等边三角形. ∴OE⊥AC, ∴BD⊥AC, ∴□ABCD是菱形;
(2)∵四边形ABCD是平行四边形, ∴AO=CO
∵△ACE是等边三角形 ∴∠AEC=∠EAC=60°,∠AED=30°,
∵∠AED=2∠EAD, ∴∠EAD=15° ∴∠DAO=∠ADO=45°,
∵四边形ABCD是菱形; ∴∠DAB=90° ∴四边形ABCD是正方形.
点睛: 此题主要考查菱形和正方形的判定,要灵活应用判定定理及等腰三角形的性质、外角的性质定理:对角线互相垂直的平行四边形是菱形;有一个角是直角的菱形是正方形;三角形的一个外角等于和它不相邻的两内角之和.

 阅读快车系列答案
阅读快车系列答案【题目】一个不透明的袋中装有红、白、黄3种颜色的若干个小球,它们除颜色外完全相同.每次从袋中摸出1个球,记下颜色后放回搅匀再摸.摸球实验中,统计得到下表中的数据:
摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
由此可以估计摸到黄球的概率约为________(精确到0.1).